discretize.TensorMesh#
- class discretize.TensorMesh(h, origin=None, **kwargs)[source]#
Tensor mesh class.
Tensor meshes are numerical grids whose cell centers, nodes, faces, edges, widths, volumes, etc… can be directly expressed as tensor products. The axes defining coordinates of the mesh are orthogonal. And cell properties along one axis do not vary with respect to the position along any other axis.
- Parameters:
- h(
dim) iterableofint,numpy.ndarray,ortuple Defines the cell widths along each axis. The length of the iterable object is equal to the dimension of the mesh (1, 2 or 3). For a 3D mesh, the list would have the form [hx, hy, hz] .
Along each axis, the user has 3 choices for defining the cells widths:
int-> A unit interval is equally discretized into N cells.numpy.ndarray-> The widths are explicity given for each cellthe widths are defined as a
listoftupleof the form (dh, nc, [npad]) where dh is the cell width, nc is the number of cells, and npad (optional) is a padding factor denoting exponential increase/decrease in the cell width for each cell; e.g. [(2., 10, -1.3), (2., 50), (2., 10, 1.3)]
- origin(
dim) iterable, default: 0 Define the origin or ‘anchor point’ of the mesh; i.e. the bottom-left-frontmost corner. By default, the mesh is anchored such that its origin is at [0, 0, 0] .
For each dimension (x, y or z), The user may set the origin 2 ways:
a
scalarwhich explicitly defines origin along that dimension.{‘0’, ‘C’, ‘N’} a
strspecifying whether the zero coordinate along each axis is the first node location (‘0’), in the center (‘C’) or the last node location (‘N’) (see Examples).
- h(
Attributes
area has been deprecated.
areaFx has been deprecated.
areaFy has been deprecated.
areaFz has been deprecated.
Averaging operator from cell centers to edges (scalar quantities).
Averaging operator from cell centers to faces (scalar quantities).
Averaging operator from cell centers to faces (vector quantities).
Averaging operator from edges to cell centers (scalar quantities).
Averaging operator from edges to cell centers (vector quantities).
Averaging operator from edges to faces.
Averaging operator from x-edges to cell centers (scalar quantities).
Averaging operator from y-edges to cell centers (scalar quantities).
Averaging operator from z-edges to cell centers (scalar quantities).
Averaging operator from faces to cell centers (scalar quantities).
Averaging operator from faces to cell centers (vector quantities).
Averaging operator from x-faces to cell centers (scalar quantities).
Averaging operator from y-faces to cell centers (scalar quantities).
Averaging operator from z-faces to cell centers (scalar quantities).
Averaging operator from nodes to cell centers (scalar quantities).
Averaging operator from nodes to edges (scalar quantities).
Averaging operator from nodes to faces (scalar quantities).
Orientation of the first axis.
Orientation of the second axis.
Orientation of the third axis.
Integrate a vector function on the boundary.
Boundary edge locations.
Outward normal vectors of boundary faces.
Represent the operation of integrating a scalar function on the boundary.
Boundary face locations.
Integrate a vector function dotted with the boundary normal.
Boundary node locations.
cellBoundaryInd has been deprecated.
cellGrad has been deprecated.
cellGradBC has been deprecated.
cellGradx has been deprecated.
cellGrady has been deprecated.
cellGradz has been deprecated.
Return the indices of the x, (y and z) boundary cells.
The bounds of each cell.
Return gridded cell center locations.
Return x-coordinates of the cell centers along the x-direction.
Return y-coordinates of the cell centers along the y-direction.
Return z-coordinates of the cell centers along the z-direction.
Cell gradient operator (cell centers to faces).
Boundary conditions matrix for the cell gradient operator (Deprecated).
X-derivative operator (cell centers to x-faces).
Y-derivative operator (cell centers to y-faces).
Z-derivative operator (cell centers to z-faces).
The index of all nodes for each cell.
Return cell volumes.
The dimension of the mesh (1, 2, or 3).
edge has been deprecated.
edgeCurl has been deprecated.
edgeEx has been deprecated.
edgeEy has been deprecated.
edgeEz has been deprecated.
Edge curl operator (edges to faces).
Return lengths of all edges in the mesh.
Unit tangent vectors for all mesh edges.
Return the x-edge lengths.
Return the y-edge lengths.
Return the z-edge lengths.
Gridded edge locations.
Gridded x-edge locations.
Gridded y-edge locations.
Gridded z-edge locations.
faceBoundaryInd has been deprecated.
faceDiv has been deprecated.
faceDivx has been deprecated.
faceDivy has been deprecated.
faceDivz has been deprecated.
Return areas of all faces in the mesh.
Return the indices of the x, (y and z) boundary faces.
Face divergence operator (faces to cell-centres).
Unit normal vectors for all mesh faces.
Return the areas of the x-faces.
X-derivative operator (x-faces to cell-centres).
Return the areas of the y-faces.
Y-derivative operator (y-faces to cell-centres).
Return the areas of the z-faces.
Z-derivative operator (z-faces to cell-centres).
Gridded face locations.
Gridded x-face locations.
Gridded y-face locations.
Gridded z-face locations.
Cell widths along each axis direction.
Return dimensions of all mesh cells as staggered grid.
Width of cells in the x direction.
Width of cells in the y direction.
Width of cells in the z direction.
Number of cells in the x direction.
Number of cells in the y direction.
Number of cells in the z direction.
Number of nodes in the x-direction.
Number of nodes in the y-direction.
Number of nodes in the z-direction.
Total number of cells in the mesh.
Total number of edges in the mesh.
The number of edges in each direction.
Number of x-edges in the mesh.
Number of y-edges in the mesh.
Number of z-edges in the mesh.
Total number of faces in the mesh.
The number of faces in each axis direction.
Number of x-faces in the mesh.
Number of y-faces in the mesh.
Number of z-faces in the mesh.
Total number of nodes in the mesh.
nodalGrad has been deprecated.
nodalLaplacian has been deprecated.
Nodal gradient operator (nodes to edges).
Nodal scalar Laplacian operator (nodes to nodes).
Return gridded node locations.
Return x-coordinates of the nodes along the x-direction.
Return y-coordinates of the nodes along the y-direction.
Return z-coordinates of the nodes along the z-direction.
normals has been deprecated.
Rotation matrix defining mesh axes relative to Cartesian.
Origin or 'anchor point' of the mesh.
Projection matrix from all edges to boundary edges.
Projection matrix from all faces to boundary faces.
Projection matrix from all nodes to boundary nodes.
Indicate whether mesh uses standard coordinate axes.
Coordinate reference system.
Alias for
orientation.Number of cells in each coordinate direction.
Number of x-edges along each axis direction.
Number of y-edges along each axis direction.
Number of z-edges along each axis direction.
Number of x-faces along each axis direction.
Number of y-faces along each axis direction.
Number of z-faces along each axis direction.
The number of nodes along each axis direction.
Stencil for cell gradient operator (cell centers to faces).
Differencing operator along x-direction (cell centers to x-faces).
Differencing operator along y-direction (cell centers to y-faces).
Differencing operator along z-direction (cell centers to z-faces).
tangents has been deprecated.
vectorCCx has been deprecated.
vectorCCy has been deprecated.
vectorCCz has been deprecated.
vectorNx has been deprecated.
vectorNy has been deprecated.
vectorNz has been deprecated.
vol has been deprecated.
Alias for the
origin.Methods
cell_gradient_weak_form_robin([alpha, beta, ...])Create Robin conditions pieces for weak form of the cell gradient operator (cell centers to faces).
closest_points_index(locations[, grid_loc, ...])Find the indicies for the nearest grid location for a set of points.
copy()Make a copy of the current mesh.
deserialize(items, **kwargs)Create this mesh from a dictionary of attributes.
edge_divergence_weak_form_robin([alpha, ...])Create Robin conditions pieces for weak form of the edge divergence operator (edges to nodes).
equals(other_mesh)Compare the current mesh with another mesh to determine if they are identical.
from_omf(element)Convert an
omfobject to adiscretizemesh.getBCProjWF(*args, **kwargs)getBCProjWF has been removed.
getBCProjWF_simple(*args, **kwargs)getBCProjWF_simple has been removed.
getEdgeInnerProduct(*args, **kwargs)getEdgeInnerProduct has been removed.
getEdgeInnerProductDeriv(*args, **kwargs)getEdgeInnerProductDeriv has been removed.
getFaceInnerProduct(*args, **kwargs)getFaceInnerProduct has been removed.
getFaceInnerProductDeriv(*args, **kwargs)getFaceInnerProductDeriv has been removed.
getInterpolationMat(*args, **kwargs)getInterpolationMat has been removed.
getTensor(*args, **kwargs)getTensor has been removed.
get_BC_projections(BC[, discretization])Create the weak form boundary condition projection matrices.
get_BC_projections_simple([discretization])Create weak form boundary condition projection matrices for mixed boundary condition.
get_edge_inner_product([model, ...])Generate the edge inner product matrix or its inverse.
get_edge_inner_product_deriv(model[, ...])Get a function handle to multiply vector with derivative of edge inner product matrix (or its inverse).
get_edge_inner_product_line([model, ...])Generate the edge inner product line matrix or its inverse.
get_edge_inner_product_line_deriv(model[, ...])Get a function handle to multiply a vector with derivative of edge inner product line matrix (or its inverse).
get_edge_inner_product_surface([model, ...])Generate the edge inner product surface matrix or its inverse.
Get a function handle to multiply a vector with derivative of edge inner product surface matrix (or its inverse).
get_face_inner_product([model, ...])Generate the face inner product matrix or its inverse.
get_face_inner_product_deriv(model[, ...])Get a function handle to multiply a vector with derivative of face inner product matrix (or its inverse).
get_face_inner_product_surface([model, ...])Generate the face inner product matrix or its inverse.
Get a function handle to multiply a vector with derivative of face inner product surface matrix (or its inverse).
get_interpolation_matrix(loc[, ...])Construct a linear interpolation matrix from mesh.
get_tensor(key)Return the base 1D arrays for a specified mesh tensor.
isInside(*args, **kwargs)isInside has been removed.
is_inside(pts[, location_type])Determine which points lie within the mesh.
plotGrid(*args, **kwargs)plotGrid has been deprecated.
plotImage(*args, **kwargs)plotImage has been deprecated.
plotSlice(*args, **kwargs)plotSlice has been deprecated.
plot_3d_slicer(v[, xslice, yslice, zslice, ...])Plot slices of a 3D volume, interactively (scroll wheel).
plot_grid([ax, nodes, faces, centers, ...])Plot the grid for nodal, cell-centered and staggered grids.
plot_image(v[, v_type, grid, view, ax, ...])Plot quantities defined on a given mesh.
plot_slice(v[, v_type, normal, ind, ...])Plot a slice of fields on the given 3D mesh.
point2index(locs)Find cells that contain the given points.
projectEdgeVector(*args, **kwargs)projectEdgeVector has been removed.
projectFaceVector(*args, **kwargs)projectFaceVector has been removed.
project_edge_vector(edge_vectors)Project vectors to the edges of the mesh.
project_face_vector(face_vectors)Project vectors onto the faces of the mesh.
r(*args, **kwargs)r has been removed.
readModelUBC(*args, **kwargs)readModelUBC has been removed.
readUBC(file_name[, directory])Read 2D or 3D tensor mesh from UBC-GIF formatted file.
readVTK(file_name[, directory])Read VTK rectilinear file (vtr or xml) and return a discretize tensor mesh (and models).
read_UBC(file_name[, directory])Read 2D or 3D tensor mesh from UBC-GIF formatted file.
read_model_UBC(file_name[, directory])Read UBC-GIF formatted model file for 2D or 3D tensor mesh.
read_vtk(file_name[, directory])Read VTK rectilinear file (vtr or xml) and return a discretize tensor mesh (and models).
reshape(x[, x_type, out_type, return_format])Reshape tensor quantities.
save([file_name, verbose])Save the mesh to json.
Represent the mesh's attributes as a dictionary.
setCellGradBC(*args, **kwargs)setCellGradBC has been removed.
Set boundary conditions for derivative operators acting on cell-centered quantities.
toVTK([models])Convert mesh (and models) to corresponding VTK or PyVista data object.
to_dict()Represent the mesh's attributes as a dictionary.
to_omf([models])Convert to an
omfdata object.to_vtk([models])Convert mesh (and models) to corresponding VTK or PyVista data object.
validate()Return the validation state of the mesh.
vtk_to_tensor_mesh(vtrGrid)Convert vtk object to a TensorMesh.
writeModelUBC(*args, **kwargs)writeModelUBC has been removed.
writeUBC(*args, **kwargs)writeUBC has been removed.
writeVTK(file_name[, models, directory])Convert mesh (and models) to corresponding VTK or PyVista data object then writes to file.
write_UBC(file_name[, models, directory, ...])Write 2D or 3D tensor mesh (and models) to UBC-GIF formatted file(s).
write_model_UBC(file_name, model[, directory])Write 2D or 3D tensor model to UBC-GIF formatted file.
write_vtk(file_name[, models, directory])Convert mesh (and models) to corresponding VTK or PyVista data object then writes to file.
See also
utils.unpack_widthsThe function used to expand a tuple to generate widths.
Examples
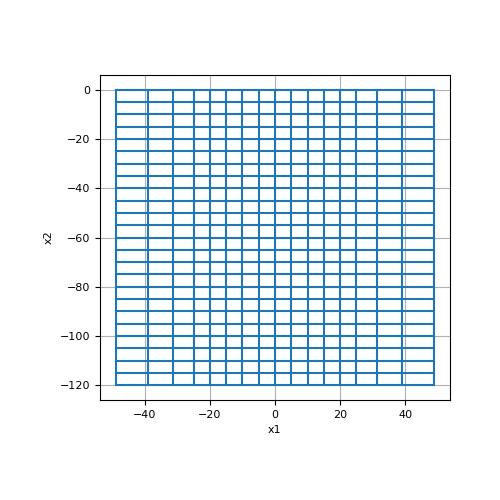
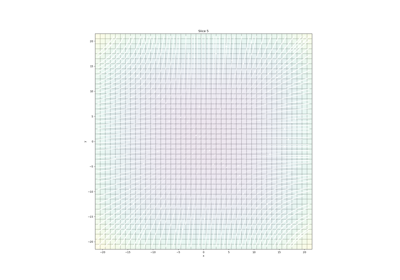
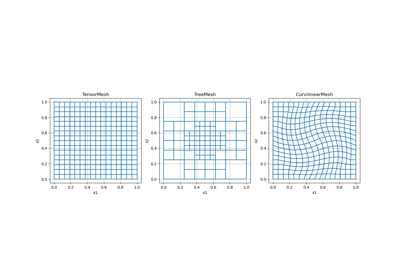
An example of a 2D tensor mesh is shown below. Here we use a list of tuple to define the discretization along the x-axis and a numpy array to define the discretization along the y-axis. We also use a string argument to center the x-axis about x = 0 and set the top of the mesh to y = 0.
>>> from discretize import TensorMesh >>> import matplotlib.pyplot as plt
>>> ncx = 10 # number of core mesh cells in x >>> dx = 5 # base cell width x >>> npad_x = 3 # number of padding cells in x >>> exp_x = 1.25 # expansion rate of padding cells in x >>> ncy = 24 # total number of mesh cells in y >>> dy = 5 # base cell width y
>>> hx = [(dx, npad_x, -exp_x), (dx, ncx), (dx, npad_x, exp_x)] >>> hy = dy * np.ones(ncy) >>> mesh = TensorMesh([hx, hy], origin='CN')
>>> fig = plt.figure(figsize=(5,5)) >>> ax = fig.add_subplot(111) >>> mesh.plot_grid(ax=ax) >>> plt.show()
(
Source code,png,pdf)