Basic Forward 2D DC Resistivity

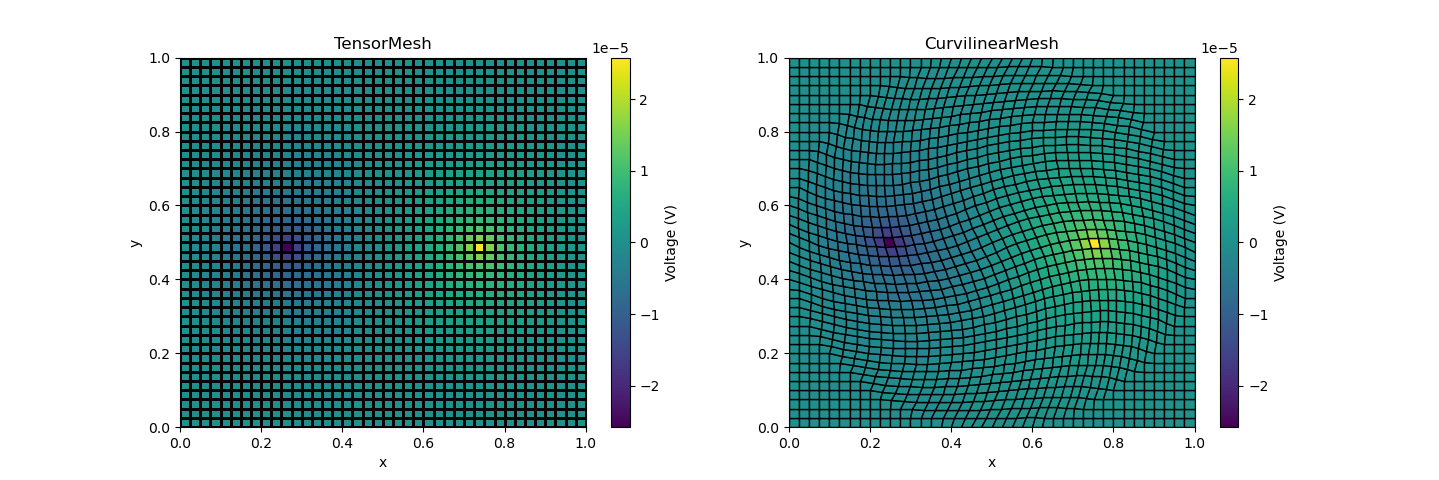
2D DC forward modeling example with Tensor and Curvilinear Meshes

/home/vsts/work/1/s/examples/plot_dc_resistivity.py:32: DeprecationWarning: The closest_points_index utilty function has been moved to be a method of a class object. Please access it as mesh.closest_points_index(). This will be removed in a future version of discretize
  txind = discretize.utils.closest_points_index(mesh, pts)

import discretize
import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse.linalg import spsolve


def run(plotIt=True):
    # Step1: Generate Tensor and Curvilinear Mesh
    sz = [40, 40]
    tM = discretize.TensorMesh(sz)
    rM = discretize.CurvilinearMesh(
        discretize.utils.example_curvilinear_grid(sz, "rotate")
    )

    # Step2: Direct Current (DC) operator
    def DCfun(mesh, pts):
        D = mesh.face_divergence
        sigma = 1e-2 * np.ones(mesh.nC)
        MsigI = mesh.get_face_inner_product(
            sigma, invert_model=True, invert_matrix=True
        )
        A = -D * MsigI * D.T
        A[-1, -1] /= mesh.cell_volumes[-1]  # Remove null space
        rhs = np.zeros(mesh.nC)
        txind = discretize.utils.closest_points_index(mesh, pts)
        rhs[txind] = np.r_[1, -1]
        return A, rhs

    pts = np.vstack((np.r_[0.25, 0.5], np.r_[0.75, 0.5]))

    # Step3: Solve DC problem (LU solver)
    AtM, rhstM = DCfun(tM, pts)
    phitM = spsolve(AtM, rhstM)

    ArM, rhsrM = DCfun(rM, pts)
    phirM = spsolve(ArM, rhsrM)

    if not plotIt:
        return

    # Step4: Making Figure
    fig, axes = plt.subplots(1, 2, figsize=(12 * 1.2, 4 * 1.2))
    vmin, vmax = phitM.min(), phitM.max()

    dat = tM.plot_image(phitM, ax=axes[0], clim=(vmin, vmax), grid=True)
    cb0 = plt.colorbar(dat[0], ax=axes[0])
    cb0.set_label("Voltage (V)")
    axes[0].set_title("TensorMesh")

    dat = rM.plot_image(phirM, ax=axes[1], clim=(vmin, vmax), grid=True)
    cb1 = plt.colorbar(dat[0], ax=axes[1])
    cb1.set_label("Voltage (V)")
    axes[1].set_title("CurvilinearMesh")


if __name__ == "__main__":
    run()
    plt.show()