discretize.TensorMesh.average_cell_to_edge#
- property TensorMesh.average_cell_to_edge#
Averaging operator from cell centers to edges (scalar quantities).
This property constructs an averaging operator that maps scalar quantities from cell centers to edge. This averaging operator is used when a discrete scalar quantity defined cell centers must be projected to edges. Once constructed, the operator is stored permanently as a property of the mesh. See notes.
- Returns:
- (
n_edges,n_cells)scipy.sparse.csr_matrix The scalar averaging operator from edges to cell centers
- (
Notes
Let \(\boldsymbol{\phi_c}\) be a discrete scalar quantity that lives at cell centers. average_cell_to_edge constructs a discrete linear operator \(\mathbf{A_{ce}}\) that projects \(\boldsymbol{\phi_c}\) to edges, i.e.:
\[\boldsymbol{\phi_e} = \mathbf{A_{ce}} \, \boldsymbol{\phi_c}\]where \(\boldsymbol{\phi_e}\) approximates the value of the scalar quantity at the edges. For each edge, we are performing a weighted average between the values at adjacent cell centers. In 1D, where adjacent cells \(i\) and \(i+1\) have widths \(h_i\) and \(h_{i+1}\), \(\phi\) on edge (node location in 1D) is approximated by:
\[\phi_{i \! + \! 1/2} \approx \frac{h_{i+1} \phi_i + h_i \phi_{i+1}}{h_i + h_{i+1}}\]On boundary edges, nearest neighbour is used to extrapolate the value from the nearest cell center. Once the operator is construct, the averaging is implemented as a matrix vector product, i.e.:
phi_e = Ace @ phi_c
Examples
Here we compute the values of a scalar function at cell centers. We then create an averaging operator to approximate the function on the edges. We choose to define a scalar function that is strongly discontinuous in some places to demonstrate how the averaging operator will smooth out discontinuities.
We start by importing the necessary packages and defining a mesh.
>>> from discretize import TensorMesh >>> import numpy as np >>> import matplotlib.pyplot as plt >>> h = np.ones(40) >>> mesh = TensorMesh([h, h], x0="CC")
Then we create a scalar variable at cell centers
>>> phi_c = np.zeros(mesh.nC) >>> xy = mesh.cell_centers >>> phi_c[(xy[:, 1] > 0)] = 25.0 >>> phi_c[(xy[:, 1] < -10.0) & (xy[:, 0] > -10.0) & (xy[:, 0] < 10.0)] = 50.0
Next, we construct the averaging operator and apply it to the discrete scalar quantity to approximate the value at the edges.
>>> Ace = mesh.average_cell_to_edge >>> phi_e = Ace @ phi_c
And plot the results:
>>> fig = plt.figure(figsize=(11, 5)) >>> ax1 = fig.add_subplot(121) >>> mesh.plot_image(phi_c, ax=ax1, v_type="CC") >>> ax1.set_title("Variable at cell centers", fontsize=16) >>> ax2 = fig.add_subplot(122) >>> mesh.plot_image(phi_e, ax=ax2, v_type="E") >>> ax2.set_title("Averaged to edges", fontsize=16) >>> plt.show()
(
Source code,png,pdf)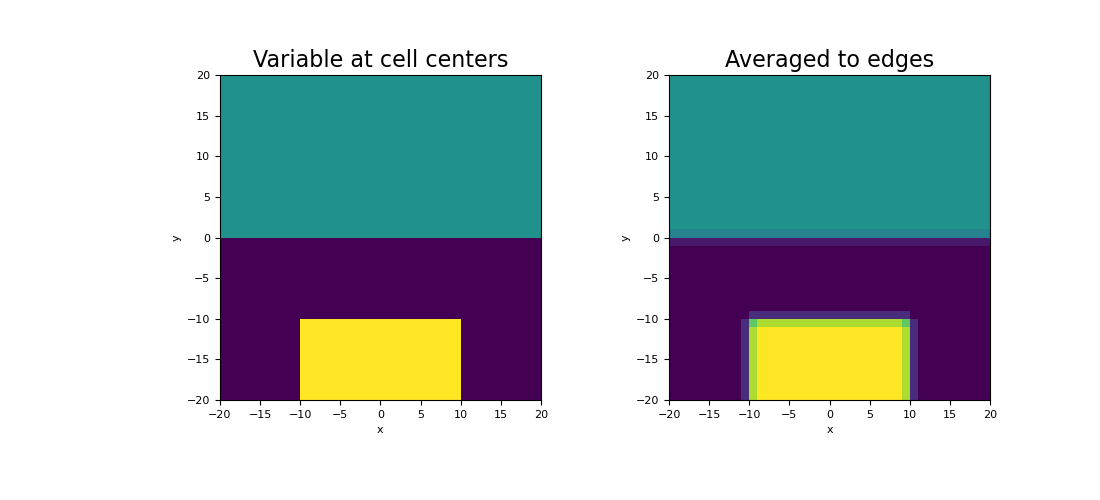
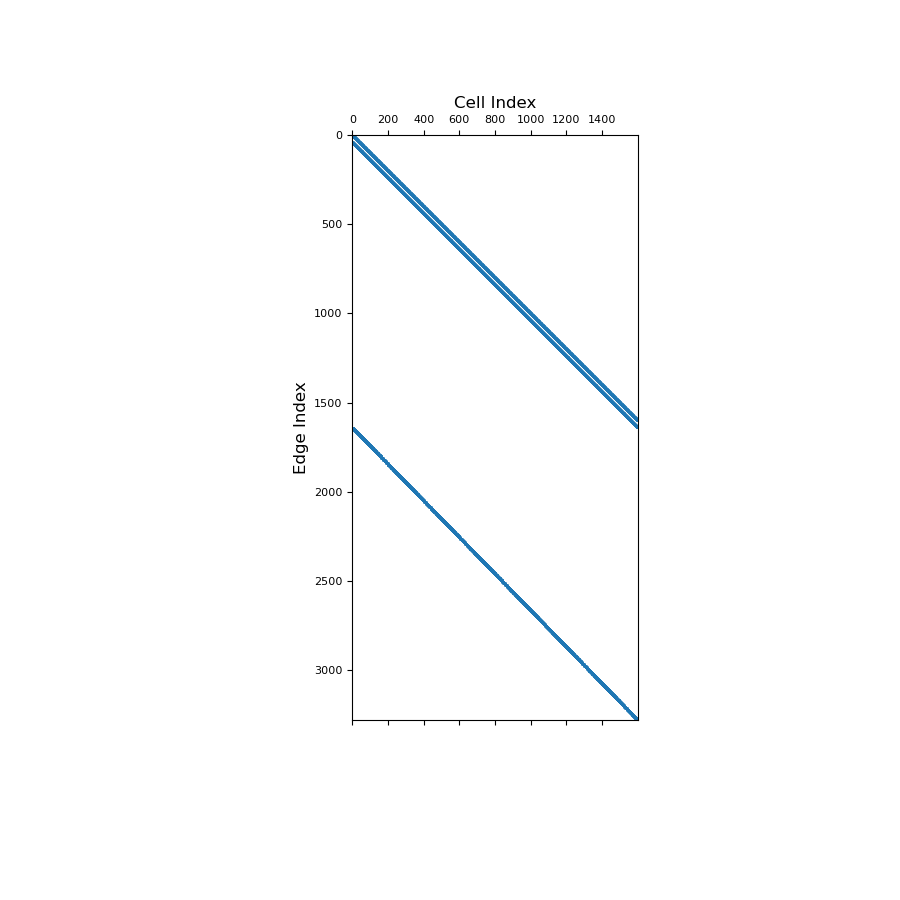
Below, we show a spy plot illustrating the sparsity and mapping of the operator.
>>> fig = plt.figure(figsize=(9, 9)) >>> ax1 = fig.add_subplot(111) >>> ax1.spy(Ace, ms=1) >>> ax1.set_title("Cell Index", fontsize=12, pad=5) >>> ax1.set_ylabel("Edge Index", fontsize=12) >>> plt.show()