discretize.CylindricalMesh#
- class discretize.CylindricalMesh(h, origin=None, cartesian_origin=None, **kwargs)[source]#
Class for cylindrical meshes.
CylindricalMeshis a mesh class for problems with rotational symmetry. It supports both cylindrically symmetric and 3D cylindrical meshes where the azimuthal discretization is user-defined. In discretize, the coordinates for cylindrical meshes are as follows:x: radial direction (\(r\))
y: azimuthal direction (\(\phi\))
z: vertical direction (\(z\))
- Parameters:
- h(
dim) iterableofint,numpy.ndarray,ortuple Defines the cell widths along each axis. The length of the iterable object is equal to the dimension of the mesh (1, 2 or 3). For a 3D mesh, the list would have the form [hr, hphi, hz] . Note that the sum of cell widths in the phi direction must equal \(2\pi\). You can also use a flat value of hphi = 1 to define a cylindrically symmetric mesh.
Along each axis, the user has 3 choices for defining the cells widths:
int-> A unit interval is equally discretized into N cells.numpy.ndarray-> The widths are explicity given for each cellthe widths are defined as a
listoftupleof the form (dh, nc, [npad]) where dh is the cell width, nc is the number of cells, and npad (optional)is a padding factor denoting exponential increase/decrease in the cell width or each cell; e.g. [(2., 10, -1.3), (2., 50), (2., 10, 1.3)]
- origin(
dim) iterable, default: 0 Define the origin or ‘anchor point’ of the mesh; i.e. the bottom-left-frontmost corner. By default, the mesh is anchored such that its origin is at
[0, 0, 0].For each dimension (r, theta or z), The user may set the origin 2 ways:
a
scalarwhich explicitly defines origin along that dimension.{‘0’, ‘C’, ‘N’} a
strspecifying whether the zero coordinate along each axis is the first node location (‘0’), in the center (‘C’) or the last node location (‘N’).
- h(
Attributes
area has been deprecated.
areaFx has been deprecated.
areaFy has been deprecated.
areaFz has been deprecated.
Averaging operator from cell centers to edges (scalar quantities).
Averaging operator from cell centers to faces (scalar quantities).
Averaging operator from cell centers to faces (vector quantities).
Averaging operator from edges to cell centers (scalar quantities).
Averaging operator from edges to cell centers (vector quantities).
Averaging operator from edges to faces.
Averaging operator from x-edges to cell centers (scalar quantities).
Averaging operator from y-edges to cell centers (scalar quantities).
Averaging operator from z-edges to cell centers (scalar quantities).
Averaging operator from faces to cell centers (scalar quantities).
Averaging operator from faces to cell centers (vector quantities).
Averaging operator from x-faces to cell centers (scalar quantities).
Averaging operator from y-faces to cell centers (scalar quantities).
Averaging operator from z-faces to cell centers (scalar quantities).
Averaging operator from nodes to cell centers (scalar quantities).
Averaging operator from nodes to edges (scalar quantities).
Averaging operator from nodes to faces (scalar quantities).
Orientation of the first axis.
Orientation of the second axis.
Orientation of the third axis.
Integrate a vector function on the boundary.
Boundary edge locations.
Outward normal vectors of boundary faces.
Represent the operation of integrating a scalar function on the boundary.
Boundary face locations.
Integrate a vector function dotted with the boundary normal.
Boundary node locations.
cartesianOrigin has been deprecated.
Cartesian origin of the mesh.
cellGrad has been deprecated.
cellGradBC has been deprecated.
cellGradx has been deprecated.
cellGrady has been deprecated.
cellGradz has been deprecated.
Return gridded cell center locations.
Return the x-positions of cell centers along the x-direction.
Return the y-positions of cell centers along the y-direction (azimuthal).
Return z-coordinates of the cell centers along the z-direction.
Cell gradient operator (cell centers to faces).
Boundary conditions matrix for the cell gradient operator (Deprecated).
X-derivative operator (cell centers to x-faces).
Y-derivative operator (cell centers to y-faces).
Z-derivative operator (cell centers to z-faces).
Volumes of all mesh cells.
The dimension of the mesh (1, 2, or 3).
edge has been deprecated.
edgeCurl has been deprecated.
edgeEx has been deprecated.
edgeEy has been deprecated.
edgeEz has been deprecated.
Edge curl operator (edges to faces).
Lengths of all mesh edges.
Unit tangent vectors for all mesh edges.
Lengths of each x edge for the entire mesh.
Arc-lengths of each y-edge for the entire mesh.
Lengths of each z-edges for the entire mesh.
Gridded edge locations.
Gridded x-edge locations.
Gridded y-edge (azimuthal edge) locations.
Gridded z-edge (vertical edge) locations.
faceDiv has been deprecated.
faceDivx has been deprecated.
faceDivy has been deprecated.
faceDivz has been deprecated.
Face areas for the entire mesh.
Face divergence operator (faces to cell-centres).
Unit normal vectors for all mesh faces.
Areas of each x-face for the entire mesh.
X-derivative operator (x-faces to cell-centres).
Areas of each y-face for the entire mesh.
Y-derivative operator (y-faces to cell-centres).
Areas of each z-face for the entire mesh.
Z-derivative operator (z-faces to cell-centres).
Gridded face locations.
Gridded x-face (radial face) locations.
Gridded y-face locations.
Gridded z-face locations.
Cell widths along each axis direction.
Return dimensions of all mesh cells as staggered grid.
Width of cells in the x direction.
Width of cells in the y direction.
Width of cells in the z direction.
Whether the radial dimension starts at 0.
isSymmetric has been deprecated.
Validate whether mesh is symmetric.
Whether the mesh discretizes the full azimuthal space.
Number of cells in the x direction.
Number of cells in the y direction.
Number of cells in the z direction.
Number of nodes in the x-direction.
Number of nodes in the y-direction.
Number of nodes in the z-direction.
Total number of cells in the mesh.
Total number of edges in the mesh.
The number of edges in each direction.
Number of x-edges in the mesh.
Number of y-edges in the mesh.
Total number of z-edges in the mesh.
Total number of faces in the mesh.
The number of faces in each axis direction.
Number of x-faces in the mesh.
Number of y-faces in the mesh.
Number of z-faces in the mesh.
Return total number of mesh nodes.
nodalGrad has been deprecated.
nodalLaplacian has been deprecated.
Nodal gradient operator (nodes to edges).
Nodal scalar Laplacian operator (nodes to nodes).
Gridded node locations.
Return the x-positions of nodes along the x-direction (radial).
Return the y-positions of nodes along the y-direction (azimuthal).
Return z-coordinates of the nodes along the z-direction.
normals has been deprecated.
Rotation matrix defining mesh axes relative to Cartesian.
Origin or 'anchor point' of the mesh.
Projection matrix from all edges to boundary edges.
Projection matrix from all faces to boundary faces.
Projection matrix from all nodes to boundary nodes.
Indicate whether mesh uses standard coordinate axes.
Coordinate reference system.
Alias for
orientation.Number of cells in each coordinate direction.
Number of x-edges along each axis direction.
Number of y-edges along each axis direction.
Number of z-edges along each axis direction.
Number of x-faces along each axis direction.
Number of y-faces along each axis direction.
Number of z-faces along each axis direction.
Return the number of nodes along each axis.
Stencil for cell gradient operator (cell centers to faces).
Differencing operator along x-direction (cell centers to x-faces).
Differencing operator along y-direction (cell centers to y-faces).
Differencing operator along z-direction (cell centers to z-faces).
tangents has been deprecated.
vectorCCx has been deprecated.
vectorCCy has been deprecated.
vectorCCz has been deprecated.
vectorNx has been deprecated.
vectorNy has been deprecated.
vectorNz has been deprecated.
vol has been deprecated.
Alias for the
origin.Methods
cartesianGrid(*args, **kwargs)cartesianGrid has been removed.
cartesian_grid([location_type, theta_shift])Return the specified grid in cartesian coordinates.
cell_gradient_weak_form_robin([alpha, beta, ...])Create Robin conditions pieces for weak form of the cell gradient operator (cell centers to faces).
closest_points_index(locations[, grid_loc, ...])Find the indicies for the nearest grid location for a set of points.
copy()Make a copy of the current mesh.
deserialize(items, **kwargs)Create this mesh from a dictionary of attributes.
edge_divergence_weak_form_robin([alpha, ...])Create Robin conditions pieces for weak form of the edge divergence operator (edges to nodes).
equals(other_mesh)Compare the current mesh with another mesh to determine if they are identical.
from_omf(element)Convert an
omfobject to adiscretizemesh.getBCProjWF(*args, **kwargs)getBCProjWF has been removed.
getBCProjWF_simple(*args, **kwargs)getBCProjWF_simple has been removed.
getEdgeInnerProduct(*args, **kwargs)getEdgeInnerProduct has been removed.
getEdgeInnerProductDeriv(*args, **kwargs)getEdgeInnerProductDeriv has been removed.
getFaceInnerProduct(*args, **kwargs)getFaceInnerProduct has been removed.
getFaceInnerProductDeriv(*args, **kwargs)getFaceInnerProductDeriv has been removed.
getInterpolationMat(*args, **kwargs)getInterpolationMat has been removed.
getInterpolationMatCartMesh(*args, **kwargs)getInterpolationMatCartMesh has been removed.
getTensor(*args, **kwargs)getTensor has been removed.
get_BC_projections(BC[, discretization])Create the weak form boundary condition projection matrices.
get_BC_projections_simple([discretization])Create weak form boundary condition projection matrices for mixed boundary condition.
get_edge_inner_product([model, ...])Generate the edge inner product matrix or its inverse.
get_edge_inner_product_deriv(model[, ...])Get a function handle to multiply vector with derivative of edge inner product matrix (or its inverse).
get_edge_inner_product_line([model, ...])Generate the edge inner product line matrix or its inverse.
get_edge_inner_product_line_deriv(model[, ...])Get a function handle to multiply a vector with derivative of edge inner product line matrix (or its inverse).
get_edge_inner_product_surface([model, ...])Generate the edge inner product surface matrix or its inverse.
Get a function handle to multiply a vector with derivative of edge inner product surface matrix (or its inverse).
get_face_inner_product([model, ...])Generate the face inner product matrix or its inverse.
get_face_inner_product_deriv(model[, ...])Get a function handle to multiply a vector with derivative of face inner product matrix (or its inverse).
get_face_inner_product_surface([model, ...])Generate the face inner product matrix or its inverse.
Get a function handle to multiply a vector with derivative of face inner product surface matrix (or its inverse).
get_interpolation_matrix(loc[, ...])Construct interpolation matrix from mesh.
Construct projection matrix from
CylindricalMeshto other mesh.get_tensor(key)Return the base 1D arrays for a specified mesh tensor.
isInside(*args, **kwargs)isInside has been removed.
is_inside(pts[, location_type])Determine which points lie within the mesh.
plotGrid(*args, **kwargs)plotGrid has been deprecated.
plotImage(*args, **kwargs)plotImage has been deprecated.
plotSlice(*args, **kwargs)plotSlice has been deprecated.
plot_3d_slicer(v[, xslice, yslice, zslice, ...])Plot slices of a 3D volume, interactively (scroll wheel).
plot_grid([ax, nodes, faces, centers, ...])Plot the grid for nodal, cell-centered and staggered grids.
plot_image(v[, v_type, grid, view, ax, ...])Plot quantities defined on a given mesh.
plot_slice(v[, v_type, normal, ind, ...])Plot a slice of fields on the given 3D mesh.
point2index(locs)Find cells that contain the given points.
projectEdgeVector(*args, **kwargs)projectEdgeVector has been removed.
projectFaceVector(*args, **kwargs)projectFaceVector has been removed.
project_edge_vector(edge_vectors)Project vectors to the edges of the mesh.
project_face_vector(face_vectors)Project vectors onto the faces of the mesh.
r(*args, **kwargs)r has been removed.
reshape(x[, x_type, out_type, return_format])Reshape tensor quantities.
save([file_name, verbose])Save the mesh to json.
Represent the mesh's attributes as a dictionary.
setCellGradBC(*args, **kwargs)setCellGradBC has been removed.
Set boundary conditions for derivative operators acting on cell-centered quantities.
toVTK([models])Convert mesh (and models) to corresponding VTK or PyVista data object.
to_dict()Represent the mesh's attributes as a dictionary.
to_omf([models])Convert to an
omfdata object.to_vtk([models])Convert mesh (and models) to corresponding VTK or PyVista data object.
validate()Return the validation state of the mesh.
writeVTK(file_name[, models, directory])Convert mesh (and models) to corresponding VTK or PyVista data object then writes to file.
write_vtk(file_name[, models, directory])Convert mesh (and models) to corresponding VTK or PyVista data object then writes to file.
Examples
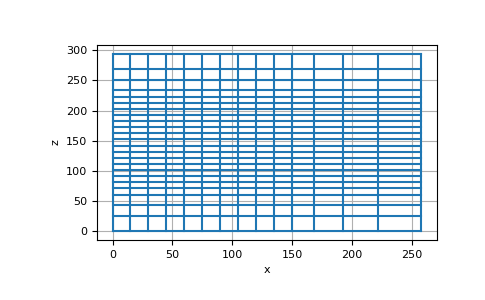
To create a general 3D cylindrical mesh, we discretize along the radial, azimuthal and vertical axis. For example:
>>> from discretize import CylindricalMesh >>> import matplotlib.pyplot as plt >>> import numpy as np
>>> ncr = 10 # number of mesh cells in r >>> ncp = 8 # number of mesh cells in phi >>> ncz = 15 # number of mesh cells in z >>> dr = 15 # cell width r >>> dz = 10 # cell width z
>>> hr = dr * np.ones(ncr) >>> hp = (2 * np.pi / ncp) * np.ones(ncp) >>> hz = dz * np.ones(ncz) >>> mesh1 = CylindricalMesh([hr, hp, hz])
>>> mesh1.plot_grid() >>> plt.show()
(
Source code,png,pdf)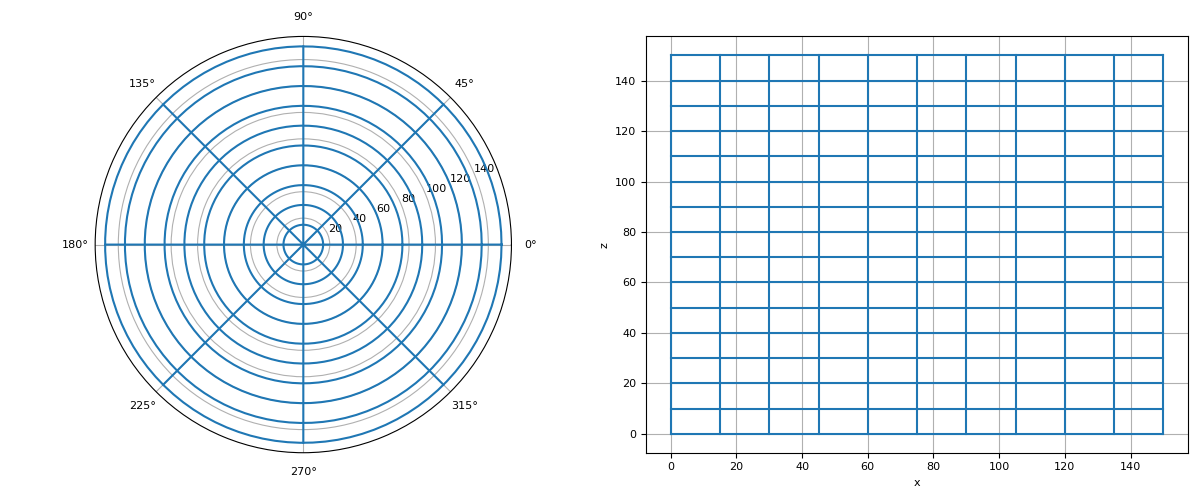
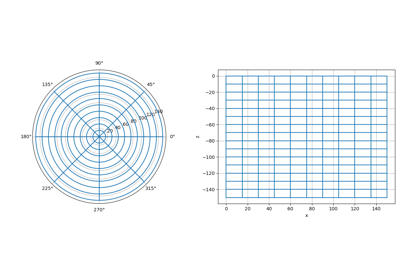
For a cylindrically symmetric mesh, the disretization along the azimuthal direction is set with a flag of 1. This reduces the size of numerical systems given that the derivative along the azimuthal direction is 0. For example:
>>> ncr = 10 # number of mesh cells in r >>> ncz = 15 # number of mesh cells in z >>> dr = 15 # cell width r >>> dz = 10 # cell width z >>> npad_r = 4 # number of padding cells in r >>> npad_z = 4 # number of padding cells in z >>> exp_r = 1.25 # expansion rate of padding cells in r >>> exp_z = 1.25 # expansion rate of padding cells in z
A value of 1 is used to define the discretization in phi for this case.
>>> hr = [(dr, ncr), (dr, npad_r, exp_r)] >>> hz = [(dz, npad_z, -exp_z), (dz, ncz), (dz, npad_z, exp_z)] >>> mesh2 = CylindricalMesh([hr, 1, hz])
>>> mesh2.plot_grid() >>> plt.show()