Constitutive Relations

When solving PDEs using the finite volume approach, inner products may contain constitutive relations; examples include Ohm’s law and Hooke’s law. For this class of inner products, you will learn how to:

• Construct the inner-product matrix in the case of isotropic and anisotropic constitutive relations

• Construct the inverse of the inner-product matrix

• Work with constitutive relations defined by the reciprocal of a parameter

Let \(\vec{J}\) and \(\vec{E}\) be two physically related quantities. If their relationship is isotropic (defined by a constant \(\sigma\)), then the constitutive relation is given by:

\[\vec{J} = \sigma \vec{E}\]

The inner product between a vector \(\vec{v}\) and the right-hand side of this expression is given by:

\[(\vec{v}, \sigma \vec{E} ) = \int_\Omega \vec{v} \cdot \sigma \vec{E} \, dv\]

Just like in the previous tutorial, we would like to approximate the inner product numerically using an inner-product matrix such that:

\[(\vec{v}, \sigma \vec{E} ) \approx \mathbf{v^T M_\sigma e}\]

where the inner product matrix \(\mathbf{M_\sigma}\) now depends on:

1. the dimensions and discretization of the mesh

2. where \(\mathbf{v}\) and \(\mathbf{e}\) live

3. the spatial distribution of the property \(\sigma\)

In the case of anisotropy, the constitutive relations are defined by a tensor (\(\Sigma\)). Here, the constitutive relation is of the form:

\[\vec{J} = \Sigma \vec{E}\]

where

\[\begin{split}\Sigma = \begin{bmatrix} \sigma_{1} & \sigma_{4} & \sigma_{5} \\ \sigma_{4} & \sigma_{2} & \sigma_{6} \\ \sigma_{5} & \sigma_{6} & \sigma_{3} \end{bmatrix}\end{split}\]

Is symmetric and defined by 6 independent parameters. The inner product between a vector \(\vec{v}\) and the right-hand side of this expression is given by:

\[(\vec{v}, \Sigma \vec{E} ) = \int_\Omega \vec{v} \cdot \Sigma \vec{E} \, dv\]

Once again we would like to approximate the inner product numerically using an inner-product matrix \(\mathbf{M_\Sigma}\) such that:

\[(\vec{v}, \Sigma \vec{E} ) \approx \mathbf{v^T M_\Sigma e}\]

Import Packages

Here we import the packages required for this tutorial

from discretize import TensorMesh
import numpy as np
import matplotlib.pyplot as plt

# sphinx_gallery_thumbnail_number = 1

Inner Product for a Single Cell

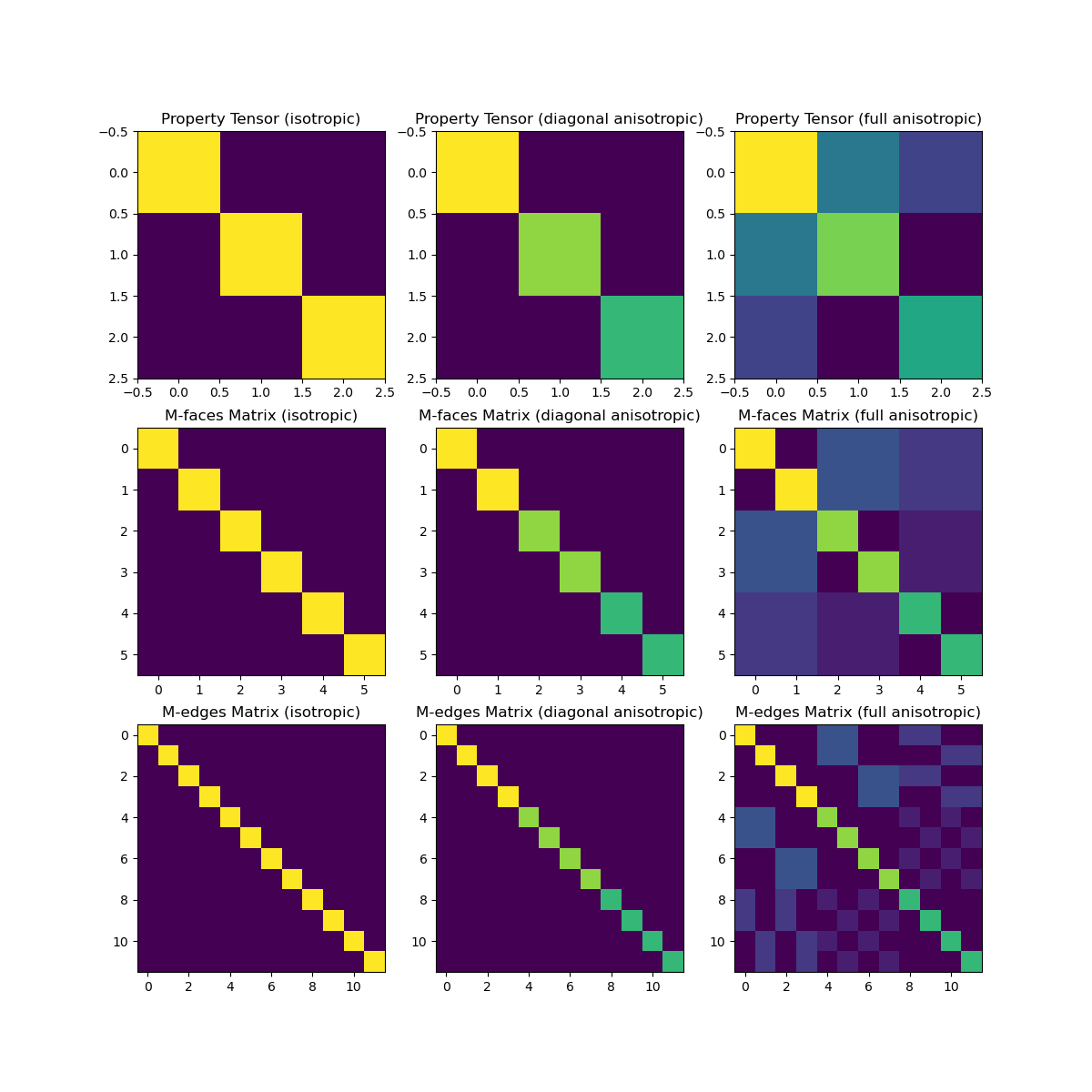
Here we compare the inner product matricies for a single cell when the constitutive relationship is:

• isotropic: \(\sigma_1 = \sigma_2 = \sigma_3 = \sigma\) and \(\sigma_4 = \sigma_5 = \sigma_6 = 0\); e.g. \(\vec{J} = \sigma \vec{E}\)

• diagonal anisotropic: independent parameters \(\sigma_1, \sigma_2, \sigma_3\) and \(\sigma_4 = \sigma_5 = \sigma_6 = 0\)

• fully anisotropic: independent parameters \(\sigma_1, \sigma_2, \sigma_3, \sigma_4, \sigma_5, \sigma_6\)

When approximating the inner product according to the finite volume approach, the constitutive parameters are defined at cell centers; even if the fields/fluxes live at cell edges/faces. As we will see, inner-product matricies are generally diagonal; except for in the fully anisotropic case where the inner product matrix contains a significant number of non-diagonal entries.

# Create a single 3D cell
h = np.ones(1)
mesh = TensorMesh([h, h, h])

# Define 6 constitutive parameters for the cell
sig1, sig2, sig3, sig4, sig5, sig6 = 6, 5, 4, 3, 2, 1

# Isotropic case
sig = sig1 * np.ones((1, 1))
sig_tensor_1 = np.diag(sig1 * np.ones(3))
Me1 = mesh.get_edge_inner_product(sig)  # Edges inner product matrix
Mf1 = mesh.get_face_inner_product(sig)  # Faces inner product matrix

# Diagonal anisotropic
sig = np.c_[sig1, sig2, sig3]
sig_tensor_2 = np.diag(np.array([sig1, sig2, sig3]))
Me2 = mesh.get_edge_inner_product(sig)
Mf2 = mesh.get_face_inner_product(sig)

# Full anisotropic
sig = np.c_[sig1, sig2, sig3, sig4, sig5, sig6]
sig_tensor_3 = np.diag(np.array([sig1, sig2, sig3]))
sig_tensor_3[(0, 1), (1, 0)] = sig4
sig_tensor_3[(0, 2), (2, 0)] = sig5
sig_tensor_3[(1, 2), (2, 1)] = sig6
Me3 = mesh.get_edge_inner_product(sig)
Mf3 = mesh.get_face_inner_product(sig)

# Plotting matrix entries
fig = plt.figure(figsize=(12, 12))

ax1 = fig.add_subplot(331)
ax1.imshow(sig_tensor_1)
ax1.set_title("Property Tensor (isotropic)")

ax2 = fig.add_subplot(332)
ax2.imshow(sig_tensor_2)
ax2.set_title("Property Tensor (diagonal anisotropic)")

ax3 = fig.add_subplot(333)
ax3.imshow(sig_tensor_3)
ax3.set_title("Property Tensor (full anisotropic)")

ax4 = fig.add_subplot(334)
ax4.imshow(Mf1.todense())
ax4.set_title("M-faces Matrix (isotropic)")

ax5 = fig.add_subplot(335)
ax5.imshow(Mf2.todense())
ax5.set_title("M-faces Matrix (diagonal anisotropic)")

ax6 = fig.add_subplot(336)
ax6.imshow(Mf3.todense())
ax6.set_title("M-faces Matrix (full anisotropic)")

ax7 = fig.add_subplot(337)
ax7.imshow(Me1.todense())
ax7.set_title("M-edges Matrix (isotropic)")

ax8 = fig.add_subplot(338)
ax8.imshow(Me2.todense())
ax8.set_title("M-edges Matrix (diagonal anisotropic)")

ax9 = fig.add_subplot(339)
ax9.imshow(Me3.todense())
ax9.set_title("M-edges Matrix (full anisotropic)")

Text(0.5, 1.0, 'M-edges Matrix (full anisotropic)')

Spatially Variant Parameters

In practice, the parameter \(\sigma\) or tensor \(\Sigma\) will vary spatially. In this case, we define the parameter \(\sigma\) (or parameters \(\Sigma\)) for each cell. When creating the inner product matrix, we enter these parameters as a numpy array. This is demonstrated below. Properties of the resulting inner product matricies are discussed.

# Create a small 3D mesh
h = np.ones(5)
mesh = TensorMesh([h, h, h])

# Isotropic case: (nC, ) numpy array
sig = np.random.rand(mesh.nC)  # sig for each cell
Me1 = mesh.get_edge_inner_product(sig)  # Edges inner product matrix
Mf1 = mesh.get_face_inner_product(sig)  # Faces inner product matrix

# Linear case: (nC, dim) numpy array
sig = np.random.rand(mesh.nC, mesh.dim)
Me2 = mesh.get_edge_inner_product(sig)
Mf2 = mesh.get_face_inner_product(sig)

# Anisotropic case: (nC, 3) for 2D and (nC, 6) for 3D
sig = np.random.rand(mesh.nC, 6)
Me3 = mesh.get_edge_inner_product(sig)
Mf3 = mesh.get_face_inner_product(sig)

# Properties of inner product matricies
print("\n FACE INNER PRODUCT MATRIX")
print("- Number of faces              :", mesh.nF)
print("- Dimensions of operator       :", str(mesh.nF), "x", str(mesh.nF))
print("- Number non-zero (isotropic)  :", str(Mf1.nnz))
print("- Number non-zero (linear)     :", str(Mf2.nnz))
print("- Number non-zero (anisotropic):", str(Mf3.nnz), "\n")

print("\n EDGE INNER PRODUCT MATRIX")
print("- Number of faces              :", mesh.nE)
print("- Dimensions of operator       :", str(mesh.nE), "x", str(mesh.nE))
print("- Number non-zero (isotropic)  :", str(Me1.nnz))
print("- Number non-zero (linear)     :", str(Me2.nnz))
print("- Number non-zero (anisotropic):", str(Me3.nnz), "\n")

 FACE INNER PRODUCT MATRIX
- Number of faces              : 450
- Dimensions of operator       : 450 x 450
- Number non-zero (isotropic)  : 450
- Number non-zero (linear)     : 450
- Number non-zero (anisotropic): 3450


 EDGE INNER PRODUCT MATRIX
- Number of faces              : 540
- Dimensions of operator       : 540 x 540
- Number non-zero (isotropic)  : 540
- Number non-zero (linear)     : 540
- Number non-zero (anisotropic): 4140

Inverse

The final discretized system using the finite volume method may contain the inverse of the inner-product matrix. Here we show how to call this using the invert_matrix keyword argument.

For the isotropic and diagonally anisotropic cases, the inner product matrix is diagonal. As a result, its inverse can be easily formed. For the full anisotropic case however, we cannot expicitly form the inverse because the inner product matrix contains a significant number of off-diagonal elements.

For the isotropic and diagonal anisotropic cases we can form \(\mathbf{M}^{-1}\) then apply it to a vector using the \(*\) operator. For the full anisotropic case, we must form the inner product matrix and do a numerical solve.

# Create a small 3D mesh
h = np.ones(5)
mesh = TensorMesh([h, h, h])

# Isotropic case: (nC, ) numpy array
sig = np.random.rand(mesh.nC)
Me1_inv = mesh.get_edge_inner_product(sig, invert_matrix=True)
Mf1_inv = mesh.get_face_inner_product(sig, invert_matrix=True)

# Diagonal anisotropic: (nC, dim) numpy array
sig = np.random.rand(mesh.nC, mesh.dim)
Me2_inv = mesh.get_edge_inner_product(sig, invert_matrix=True)
Mf2_inv = mesh.get_face_inner_product(sig, invert_matrix=True)

# Full anisotropic: (nC, 3) for 2D and (nC, 6) for 3D
sig = np.random.rand(mesh.nC, 6)
Me3 = mesh.get_edge_inner_product(sig)
Mf3 = mesh.get_face_inner_product(sig)

Reciprocal Properties

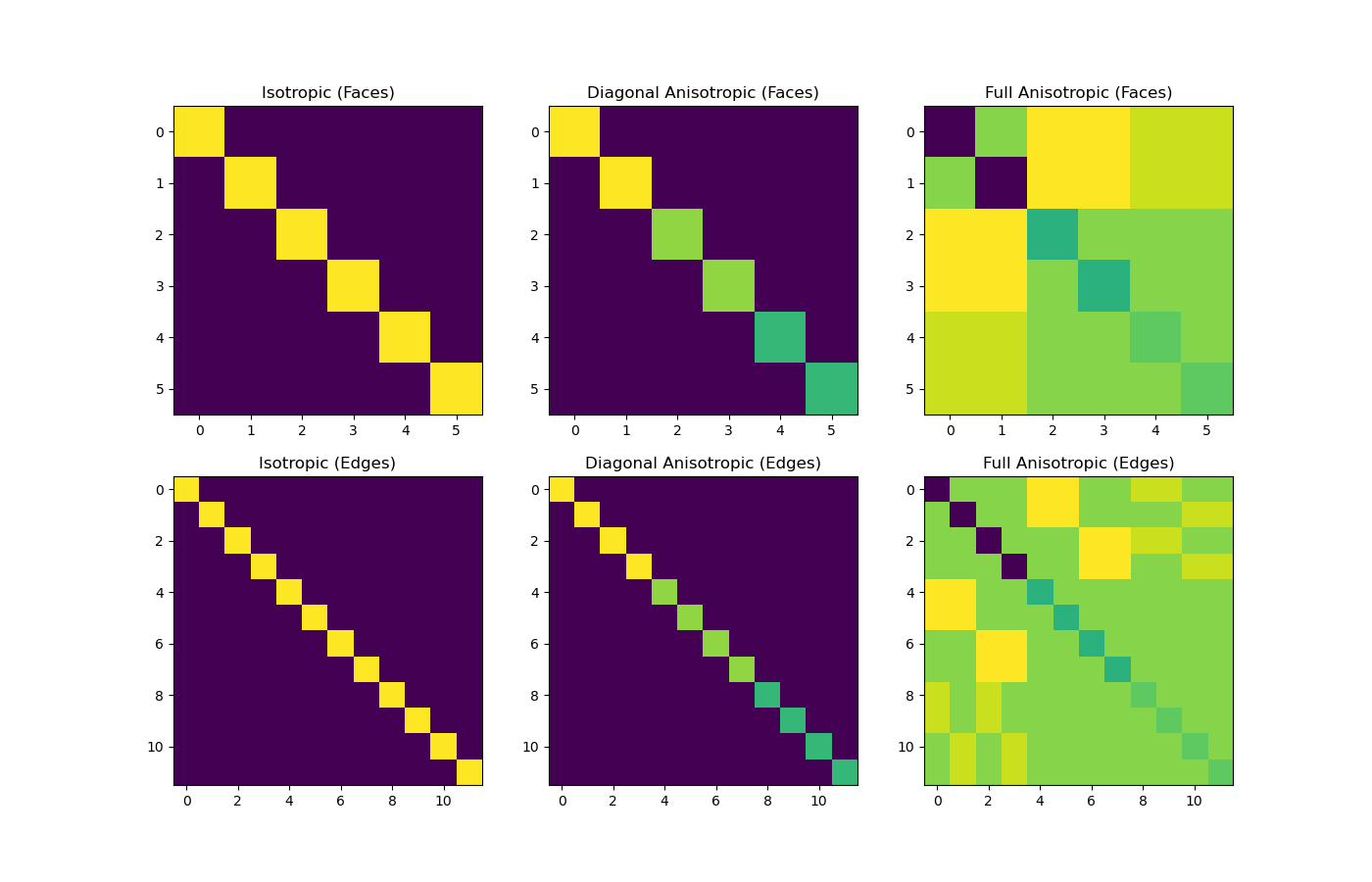
At times, the constitutive relation may be defined by the reciprocal of a parameter (\(\rho\)). Here we demonstrate how inner product matricies can be formed using the keyword argument invert_model. We will do this for a single cell and plot the matrix elements. We can easily extend this to a mesh comprised of many cells.

In this case, the constitutive relation is given by:

\[\vec{J} = \frac{1}{\rho} \vec{E}\]

The inner product between a vector \(\vec{v}\) and the right-hand side of the expression is given by:

\[(\vec{v}, \rho^{-1} \vec{E} ) = \int_\Omega \vec{v} \cdot \rho^{-1} \vec{E} \, dv\]

where the inner product is approximated using an inner product matrix \(\mathbf{M_{\rho^{-1}}}\) as follows:

\[(\vec{v}, \rho^{-1} \vec{E} ) \approx \mathbf{v^T M_{\rho^{-1}} e}\]

In the case that the constitutive relation is defined by a tensor \(P\), e.g.:

\[\vec{J} = P \vec{E}\]

where

\[\begin{split}P = \begin{bmatrix} \rho_{1}^{-1} & \rho_{4}^{-1} & \rho_{5}^{-1} \\ \rho_{4}^{-1} & \rho_{2}^{-1} & \rho_{6}^{-1} \\ \rho_{5}^{-1} & \rho_{6}^{-1} & \rho_{3}^{-1} \end{bmatrix}\end{split}\]

The inner product between a vector \(\vec{v}\) and the right-hand side of this expression is given by:

\[(\vec{v}, P \vec{E} ) = \int_\Omega \vec{v} \cdot P \vec{E} \, dv\]

Once again we would like to approximate the inner product numerically using an inner-product matrix \(\mathbf{M_P}\) such that:

\[(\vec{v}, P \vec{E} ) \approx \mathbf{v^T M_P e}\]

Here we demonstrate how to form the inner-product matricies \(\mathbf{M_{\rho^{-1}}}\) and \(\mathbf{M_P}\).

# Create a small 3D mesh
h = np.ones(1)
mesh = TensorMesh([h, h, h])

# Define 6 constitutive parameters for the cell
rho1, rho2, rho3, rho4, rho5, rho6 = (
    1.0 / 6.0,
    1.0 / 5.0,
    1.0 / 4.0,
    1.0 / 3.0,
    1.0 / 2.0,
    1,
)

# Isotropic case
rho = rho1 * np.ones((1, 1))
Me1 = mesh.get_edge_inner_product(rho, invert_model=True)  # Edges inner product matrix
Mf1 = mesh.get_face_inner_product(rho, invert_model=True)  # Faces inner product matrix

# Diagonal anisotropic case
rho = np.c_[rho1, rho2, rho3]
Me2 = mesh.get_edge_inner_product(rho, invert_model=True)
Mf2 = mesh.get_face_inner_product(rho, invert_model=True)

# Full anisotropic case
rho = np.c_[rho1, rho2, rho3, rho4, rho5, rho6]
Me3 = mesh.get_edge_inner_product(rho, invert_model=True)
Mf3 = mesh.get_face_inner_product(rho, invert_model=True)

# Plotting matrix entries
fig = plt.figure(figsize=(14, 9))

ax1 = fig.add_subplot(231)
ax1.imshow(Mf1.todense())
ax1.set_title("Isotropic (Faces)")

ax2 = fig.add_subplot(232)
ax2.imshow(Mf2.todense())
ax2.set_title("Diagonal Anisotropic (Faces)")

ax3 = fig.add_subplot(233)
ax3.imshow(Mf3.todense())
ax3.set_title("Full Anisotropic (Faces)")

ax4 = fig.add_subplot(234)
ax4.imshow(Me1.todense())
ax4.set_title("Isotropic (Edges)")

ax5 = fig.add_subplot(235)
ax5.imshow(Me2.todense())
ax5.set_title("Diagonal Anisotropic (Edges)")

ax6 = fig.add_subplot(236)
ax6.imshow(Me3.todense())
ax6.set_title("Full Anisotropic (Edges)")

Text(0.5, 1.0, 'Full Anisotropic (Edges)')