discretize.TreeMesh.refine_vertical_trianglular_prism#
- TreeMesh.refine_vertical_trianglular_prism(self, triangle, h, levels, finalize=True, diagonal_balance=None)#
Refine the
TreeMeshalong the trianglular prism to the desired level.Refines the TreeMesh by determining if a cell intersects the given trianglular prism(s) to the prescribed level(s).
- Parameters:
- triangle(
N, 3,dim) array_like The nodes of the bottom triangle(s).
- h(
N) array_like The height of the prism(s).
- levels
intor(N) array_likeofint The level to refine intersecting cells to.
- finalizebool,
optional Whether to finalize after refining
- diagonal_balancebool or
None,optional Whether to balance cells diagonally in the refinement, None implies using the same setting used to instantiate the TreeMesh`.
- triangle(
See also
Examples
We create a simple mesh and refine the TreeMesh such that all cells that intersect the line segment path are at the given levels.
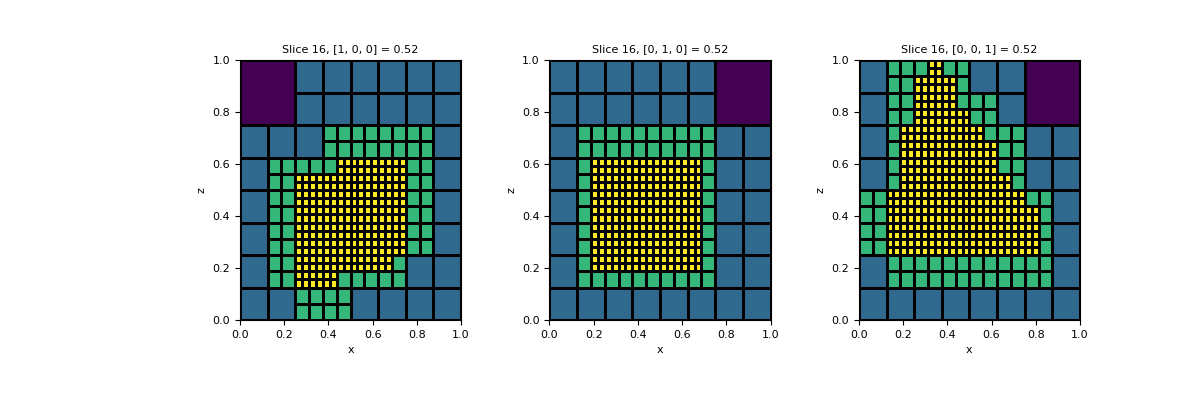
>>> import discretize >>> import matplotlib.pyplot as plt >>> import matplotlib.patches as patches >>> mesh = discretize.TreeMesh([32, 32, 32]) >>> mesh.max_level 5
Next we define the bottom points of the prism, its heights, and the level we want to refine to, then refine the mesh.
>>> triangle = [[0.14, 0.31, 0.21], [0.32, 0.96, 0.34], [0.87, 0.23, 0.12]] >>> height = 0.35 >>> levels = 5 >>> mesh.refine_vertical_trianglular_prism(triangle, height, levels)
Now lets look at the mesh.
>>> v = mesh.cell_levels_by_index(np.arange(mesh.n_cells)) >>> fig, axs = plt.subplots(1, 3, figsize=(12,4)) >>> mesh.plot_slice(v, ax=axs[0], normal='x', grid=True, clim=[2, 5]) >>> mesh.plot_slice(v, ax=axs[1], normal='y', grid=True, clim=[2, 5]) >>> mesh.plot_slice(v, ax=axs[2], normal='z', grid=True, clim=[2, 5]) >>> plt.show()
(
Source code,png,pdf)