discretize.TreeMesh.refine_surface

TreeMesh.refine_surface(xyz, level=-1, padding_cells_by_level=None, pad_up=False, pad_down=True, finalize=True, diagonal_balance=None, extrapolate_surface=None)

Refine along a surface triangulated from xyz to the prescribed level.

This function refines the mesh based on a triangulated surface from the input points. Every cell that intersects the surface will be refined to the given level.

It also optionally pads the surface at each level based on the number of padding cells at each dimension. Vertically, the surface is shifted down (and/or up) by the padding amount. Horizontally, the padding is done in one of two ways, set by extrapolate_surface. If False (the current default), the bounding box of the surface is stretched in each dimension. If True, points are added outward from every node along the boundary of the triangulation, along the outward bisector of the adjacent boundary edges (equivalent to a nearest neighbor extrapolation of the surface), see extend_surface_boundary().

Parameters:

xyz(N, dim) array_like or tuple

The points defining the surface. Will be triangulated along the horizontal dimensions. You are able to supply your own triangulation in 3D by passing a tuple of (xyz, triangle_indices).

levelint, optional

The level of the tree mesh to refine to. Negative values index tree levels backwards, (e.g. -1 is max_level).

padding_cells_by_levelNone, int, (n_level) array_like or (n_level, dim) array_like, optional

The number of cells to pad the bounding box at each level of refinement. If a single number, each level below level will be padded with those number of cells. If array_like, n_level`s below ``level` will be padded, where if a 1D array, each dimension will be padded with the same number of cells, or 2D array supports variable padding along each dimension. None implies no padding.

pad_upbool, optional

Whether to pad above the surface.

pad_downbool, optional

Whether to pad below the surface.

finalizebool, optional

Whether to finalize the mesh after the call.

diagonal_balanceNone or bool, optional

Whether to balance cells diagonally in the refinement, None implies using the same setting used to instantiate the TreeMesh`.

extrapolate_surfaceNone or bool, optional

Whether to pad horizontally by extrapolating the surface outward from the nodes on its boundary, instead of stretching its bounding box. None implies False, but issues a warning if horizontal padding is requested, as the default will change to True in discretize v1.0. This has no effect if there is no horizontal padding.

See also

refine_triangle, refine_vertical_trianglular_prism, discretize.utils.extend_surface_boundary

Notes

When extrapolate_surface=True and the surface has a non-convex boundary, the outward bisectors of different boundary nodes can intersect if the horizontal padding is large compared to the size of local features of the boundary (e.g. notches or concavities). In that case the padded region can fold over itself and the result may be unreliable. Keep the padding small relative to such features, or use a convex boundary.

Examples

In 2D we define the surface as a line segment, which we would like to refine along.

>>> import discretize
>>> import matplotlib.pyplot as plt
>>> import matplotlib.patches as patches
>>> mesh = discretize.TreeMesh([32, 32])

This surface is a simple sine curve, which we would like to pad with at least 2 cells vertically below at the maximum level, and 3 cells below that at the second highest level.

>>> x = np.linspace(0.2, 0.8, 51)
>>> z = 0.25*np.sin(2*np.pi*x)+0.5
>>> xz = np.c_[x, z]
>>> mesh.refine_surface(xz, -1, [[0, 2], [0, 3]])

>>> ax = mesh.plot_grid()
>>> ax.plot(x, z, color='C1')
>>> plt.show()

(Source code, png, pdf)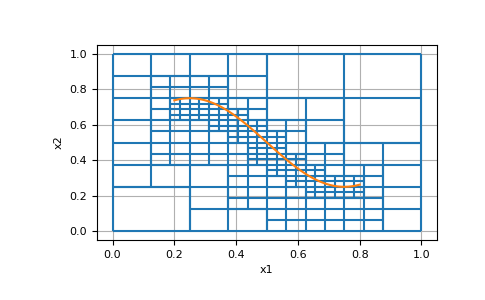

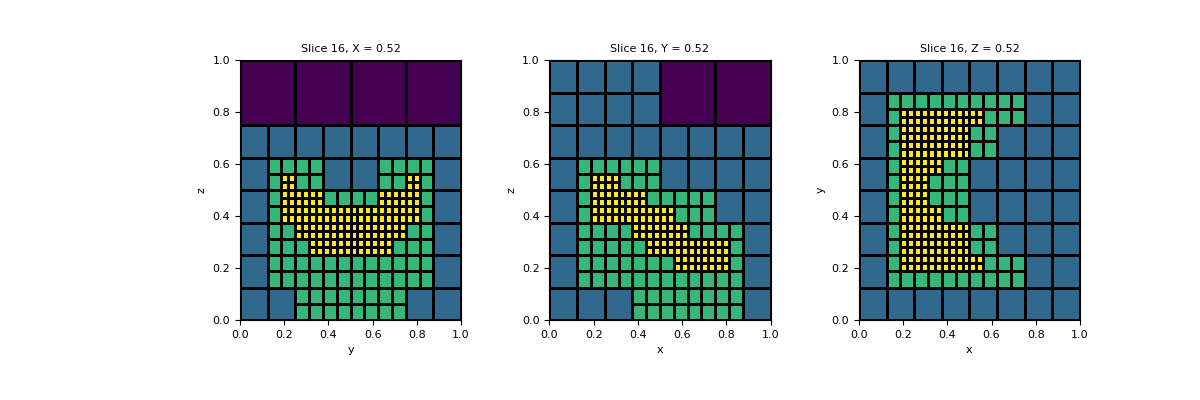
In 3D we define a grid of surface locations with there corresponding elevations. In this example we pad 2 cells at the finest level below the surface, and 3 cells down at the next level.

>>> mesh = discretize.TreeMesh([32, 32, 32])
>>> x, y = np.mgrid[0.2:0.8:21j, 0.2:0.8:21j]
>>> z = 0.125*np.sin(2*np.pi*x) + 0.5 + 0.125 * np.cos(2 * np.pi * y)
>>> points = np.stack([x, y, z], axis=-1).reshape(-1, 3)
>>> mesh.refine_surface(points, -1, [[0, 0, 2], [0, 0, 3]])

>>> v = mesh.cell_levels_by_index(np.arange(mesh.n_cells))
>>> fig, axs = plt.subplots(1, 3, figsize=(12,4))
>>> mesh.plot_slice(v, ax=axs[0], normal='x', grid=True, clim=[2, 5])
>>> mesh.plot_slice(v, ax=axs[1], normal='y', grid=True, clim=[2, 5])
>>> mesh.plot_slice(v, ax=axs[2], normal='z', grid=True, clim=[2, 5])
>>> plt.show()

(png, pdf)