discretize.TreeMesh.refine_ball

TreeMesh.refine_ball(self, points, radii, levels, finalize=True, diagonal_balance=None)

Refine TreeMesh using radial distance (ball) and refinement level for a cluster of points.

For each point in the array points, this method refines the tree mesh based on the radial distance (ball) and refinement level supplied. The method accomplishes this by determining which cells intersect ball(s) and refining them to the prescribed level(s) of refinement.

Parameters:

points(N, dim) array_like

The centers of the refinement balls

radiifloat or (N) array_like of float

A 1D array defining the radius for each ball

levelsint or (N) array_like of int

A 1D array defining the maximum refinement level for each ball

finalizebool, optional

Whether to finalize after refining

diagonal_balancebool or None, optional

Whether to balance cells diagonally in the refinement, None implies using the same setting used to instantiate the TreeMesh`.

Examples

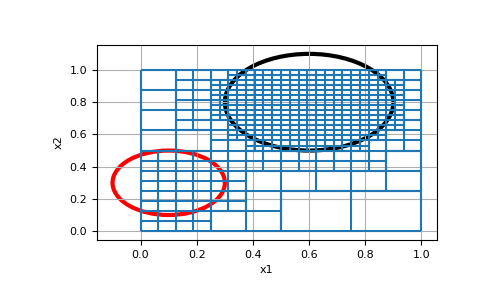
We create a simple mesh and refine the tree mesh such that all cells that intersect the spherical balls are at the given levels.

>>> import discretize
>>> import matplotlib.pyplot as plt
>>> import matplotlib.patches as patches
>>> tree_mesh = discretize.TreeMesh([32, 32])
>>> tree_mesh.max_level
5

Next we define the center and radius of the two spheres, as well as the level we want to refine them to, and refine the mesh.

>>> centers = [[0.1, 0.3], [0.6, 0.8]]
>>> radii = [0.2, 0.3]
>>> levels = [4, 5]
>>> tree_mesh.refine_ball(centers, radii, levels)

Now lets look at the mesh, and overlay the balls on it to ensure it refined where we wanted it to.

>>> ax = tree_mesh.plot_grid()
>>> circ = patches.Circle(centers[0], radii[0], facecolor='none', edgecolor='r', linewidth=3)
>>> ax.add_patch(circ)
>>> circ = patches.Circle(centers[1], radii[1], facecolor='none', edgecolor='k', linewidth=3)
>>> ax.add_patch(circ)
>>> plt.show()

(Source code, png, pdf)