discretize.SimplexMesh

class discretize.SimplexMesh(nodes, simplices)

Class for traingular (2D) and tetrahedral (3D) meshes.

Simplex is the abstract term for triangular like elements in an arbitrary dimension. Simplex meshes are subdivided into trianglular (in 2D) or tetrahedral (in 3D) elements. They are capable of representing abstract geometric surfaces, with widely variable element sizes.

Parameters:

nodes(n_nodes, dim) array_like of float

Defines every node of the mesh.

simplices(n_cells, dim+1) array_like of int

This array defines the connectivity of nodes to form cells. Each element indexes into the nodes array. Each row defines which nodes make a given cell. This array is sorted along each row and then stored on the mesh.

Attributes

area	area has been deprecated.
average_cell_to_edge	Averaging operator from cell centers to edges (scalar quantities).
average_cell_to_face	Averaging operator from cell centers to faces (scalar quantities).
average_cell_to_node	Averaging matrix from cell centers to nodes.
average_cell_vector_to_face	Averaging operator from cell centers to faces (vector quantities).
average_edge_to_cell	Averaging operator from edges to cell centers (scalar quantities).
average_edge_to_cell_vector	Averaging operator from edges to cell centers (vector quantities).
average_edge_to_face	Averaging operator from edges to faces.
average_face_to_cell	Averaging operator from faces to cell centers (scalar quantities).
average_face_to_cell_vector	Averaging operator from faces to cell centers (vector quantities).
average_node_to_cell	Averaging operator from nodes to cell centers (scalar quantities).
average_node_to_edge	Averaging operator from nodes to edges (scalar quantities).
average_node_to_face	Averaging operator from nodes to faces (scalar quantities).
boundary_edge_vector_integral	Represent the operation of integrating a vector function on the boundary.
boundary_edges	Boundary edge locations.
boundary_face_list	Boolean array of faces that lie on the boundary of the mesh.
boundary_face_outward_normals	Outward normal vectors of boundary faces.
boundary_face_scalar_integral	Represent the operation of integrating a scalar function on the boundary.
boundary_faces	Boundary face locations.
boundary_node_vector_integral	Represent the operation of integrating a vector function dotted with the boundary normal.
boundary_nodes	Boundary node locations.
cell_centers	Return gridded cell center locations.
cell_centers_tree	A KDTree object built from the cell centers.
cell_volumes	Return cell volumes.
dim	The dimension of the mesh (1, 2, or 3).
edge	edge has been deprecated.
edgeCurl	edgeCurl has been deprecated.
edge_curl	Edge curl operator (edges to faces).
edge_lengths	Return lengths of all edges in the mesh.
edge_tangents	Unit tangent vectors for all mesh edges.
edges	Gridded edge locations.
faceDiv	faceDiv has been deprecated.
face_areas	Return areas of all faces in the mesh.
face_divergence	Face divergence operator (faces to cell-centres).
face_normals	Unit normal vectors for all mesh faces.
faces	Gridded face locations.
n_cells	Total number of cells in the mesh.
n_edges	Total number of edges in the mesh.
n_faces	Total number of faces in the mesh.
n_nodes	Total number of nodes in the mesh.
neighbors	The adjacancy graph of the mesh.
nodalGrad	nodalGrad has been deprecated.
nodalLaplacian	nodalLaplacian has been deprecated.
nodal_gradient	Nodal gradient operator (nodes to edges).
nodal_laplacian	Nodal scalar Laplacian operator (nodes to nodes).
nodes	Return gridded node locations.
normals	normals has been deprecated.
project_edge_to_boundary_edge	Projection matrix from all edges to boundary edges.
project_face_to_boundary_face	Projection matrix from all faces to boundary faces.
project_node_to_boundary_node	Projection matrix from all nodes to boundary nodes.
simplices	The node indices for all simplexes of the mesh.
stencil_cell_gradient	Stencil for cell gradient operator (cell centers to faces).
tangents	tangents has been deprecated.
transform_and_shift	The barycentric transformation matrix and shift.
vol	vol has been deprecated.

Methods

closest_points_index(locations[, grid_loc, ...])	Find the indicies for the nearest grid location for a set of points.
copy()	Make a copy of the current mesh.
deserialize(items, **kwargs)	Create this mesh from a dictionary of attributes.
equals(other_mesh)	Compare the current mesh with another mesh to determine if they are identical.
from_omf(element)	Convert an omf object to a discretize mesh.
getEdgeInnerProduct(*args, **kwargs)	getEdgeInnerProduct has been removed.
getEdgeInnerProductDeriv(*args, **kwargs)	getEdgeInnerProductDeriv has been removed.
getFaceInnerProduct(*args, **kwargs)	getFaceInnerProduct has been removed.
getFaceInnerProductDeriv(*args, **kwargs)	getFaceInnerProductDeriv has been removed.
getInterpolationMat(*args, **kwargs)	getInterpolationMat has been removed.
get_edge_inner_product([model, ...])	Generate the edge inner product matrix or its inverse.
get_edge_inner_product_deriv(model[, ...])	Get a function handle to multiply vector with derivative of edge inner product matrix (or its inverse).
get_edge_inner_product_line([model, ...])	Generate the edge inner product line matrix or its inverse.
get_edge_inner_product_line_deriv(model[, ...])	Get a function handle to multiply a vector with derivative of edge inner product line matrix (or its inverse).
get_edge_inner_product_surface([model, ...])	Generate the edge inner product surface matrix or its inverse.
get_edge_inner_product_surface_deriv(model)	Get a function handle to multiply a vector with derivative of edge inner product surface matrix (or its inverse).
get_face_inner_product([model, ...])	Generate the face inner product matrix or its inverse.
get_face_inner_product_deriv(model[, ...])	Get a function handle to multiply a vector with derivative of face inner product matrix (or its inverse).
get_face_inner_product_surface([model, ...])	Generate the face inner product matrix or its inverse.
get_face_inner_product_surface_deriv(model)	Get a function handle to multiply a vector with derivative of face inner product surface matrix (or its inverse).
get_interpolation_matrix(loc[, ...])	Construct a linear interpolation matrix from mesh.
plotGrid(*args, **kwargs)	plotGrid has been deprecated.
plotImage(*args, **kwargs)	plotImage has been deprecated.
plotSlice(*args, **kwargs)	plotSlice has been deprecated.
plot_3d_slicer(v[, xslice, yslice, zslice, ...])	Plot slices of a 3D volume, interactively (scroll wheel).
plot_grid([ax, nodes, faces, centers, ...])	Plot the grid for nodal, cell-centered and staggered grids.
plot_image(v[, v_type, grid, view, ax, ...])	Plot quantities defined on a given mesh.
plot_slice(v[, v_type, normal, ind, ...])	Plot a slice of fields on the given 3D mesh.
point2index(locs)	Find cells that contain the given points.
projectEdgeVector(*args, **kwargs)	projectEdgeVector has been removed.
projectFaceVector(*args, **kwargs)	projectFaceVector has been removed.
project_edge_vector(edge_vectors)	Project vectors to the edges of the mesh.
project_face_vector(face_vectors)	Project vectors onto the faces of the mesh.
read_vtk(file_name[, directory])	Read VTK unstructured file (vtu or xml) and return a discretize simplex mesh (and models).
save([file_name, verbose])	Save the mesh to json.
serialize()	Represent the mesh's attributes as a dictionary.
toVTK([models])	Convert mesh (and models) to corresponding VTK or PyVista data object.
to_dict()	Represent the mesh's attributes as a dictionary.
to_omf([models])	Convert to an omf data object.
to_vtk([models])	Convert mesh (and models) to corresponding VTK or PyVista data object.
validate()	Return the validation state of the mesh.
vtk_to_simplex_mesh(vtuGrid)	Convert an unstructured grid of simplices to a SimplexMesh.
writeVTK(file_name[, models, directory])	Convert mesh (and models) to corresponding VTK or PyVista data object then writes to file.
write_vtk(file_name[, models, directory])	Convert mesh (and models) to corresponding VTK or PyVista data object then writes to file.

Notes

Only rudimentary checking of the input nodes and simplices is performed, only checking for degenerate simplices who have zero volume. There are no checks for overlapping cells, or for the quality of the mesh.

Examples

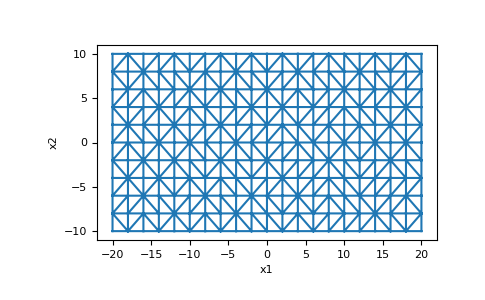
Here we generate a basic 2D triangular mesh, by triangulating a rectangular domain.

>>> from discretize import SimplexMesh
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import matplotlib.tri as tri

First we define the nodes of our mesh

>>> X, Y = np.mgrid[-20:20:21j, -10:10:11j]
>>> nodes = np.c_[X.reshape(-1), Y.reshape(-1)]

Then we triangulate the nodes, here we use matplotlib, but you could also use scipy’s Delaunay, or any other triangular mesh generator. Essentailly we are creating every node in the mesh, and a list of triangles/tetrahedrals defining which nodes make of each cell.

>>> triang = tri.Triangulation(nodes[:, 0], nodes[:, 1])
>>> simplices = triang.triangles

Finally we can assemble them into a SimplexMesh

>>> mesh = SimplexMesh(nodes, simplices)
>>> mesh.plot_grid()
>>> plt.show()

(Source code, png, pdf)