discretize.utils.extract_core_mesh

discretize.utils.extract_core_mesh(xyzlim, mesh, mesh_type='tensor')

Extract the core mesh from a global mesh.

Parameters:

xyzlim(dim, 2) numpy.ndarray

2D array defining the x, y and z cutoffs for the core mesh region. Each row contains the minimum and maximum limit for the x, y and z axis, respectively.

meshdiscretize.TensorMesh

The mesh

mesh_typestr, optional

Unused currently

Returns:

tuple: (active_index, core_mesh)

active_index is a boolean array that maps from the global the mesh to core mesh. core_mesh is a discretize.base.BaseMesh object representing the core mesh.

Examples

Here, we define a 2D tensor mesh that has both a core region and padding. We use the function extract_core_mesh to return a mesh which contains only the core region.

>>> from discretize.utils import extract_core_mesh
>>> from discretize import TensorMesh
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import matplotlib as mpl
>>> mpl.rcParams.update({"font.size": 14})

Form a mesh of a uniform cube

>>> h = [(1., 5, -1.5), (1., 20), (1., 5, 1.5)]
>>> mesh = TensorMesh([h, h], origin='CC')

Plot original mesh

>>> fig = plt.figure(figsize=(7, 7))
>>> ax = fig.add_subplot(111)
>>> mesh.plot_grid(ax=ax)
>>> ax.set_title('Original Tensor Mesh')
>>> plt.show()

(Source code, png, pdf)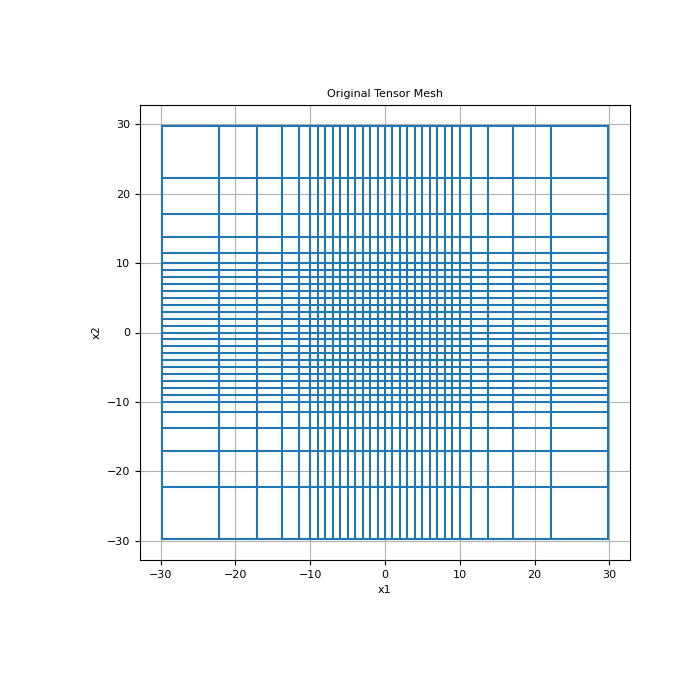

Set the limits for the cutoff of the core mesh (dim, 2)

>>> xlim = np.c_[-10., 10]
>>> ylim = np.c_[-10., 10]
>>> core_limits = np.r_[xlim, ylim]

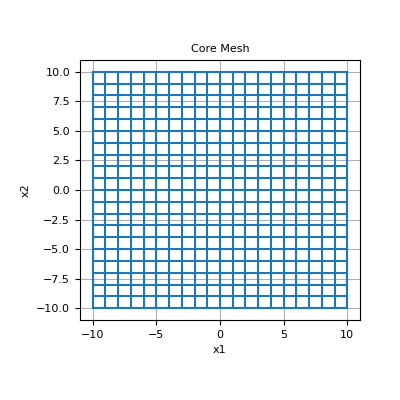
Extract indices of core mesh cells and the core mesh, then plot

>>> core_ind, core_mesh = extract_core_mesh(core_limits, mesh)
>>> fig = plt.figure(figsize=(4, 4))
>>> ax = fig.add_subplot(111)
>>> core_mesh.plot_grid(ax=ax)
>>> ax.set_title('Core Mesh')
>>> plt.show()

(png, pdf)