discretize.utils.refine_tree_xyz#
- discretize.utils.refine_tree_xyz(mesh, xyz, method='radial', octree_levels=(1, 1, 1), octree_levels_padding=None, finalize=False, min_level=0, max_distance=inf)[source]#
Refine region within a
TreeMesh.This function refines the specified region of a tree mesh using one of several methods. These are summarized below:
radial: refines based on radial distances from a set of xy[z] locations. Consider a tree mesh whose smallest cell size has a width of h . And octree_levels = [nc1, nc2, nc3, …] . Within a distance of nc1 x h from any of the points supplied, the smallest cell size is used. Within a distance of nc2 x (2h) , the cells will have a width of 2h . Within a distance of nc3 x (4h) , the cells will have a width of 4h . Etc…
surface: refines downward from a triangulated surface. Consider a tree mesh whose smallest cell size has a width of h. And octree_levels = [nc1, nc2, nc3, …] . Within a downward distance of nc1 x h from the topography (xy[z] ) supplied, the smallest cell size is used. The topography is triangulated if the points supplied are coarser than the cell size. No refinement is done above the topography. Within a vertical distance of nc2 x (2h) , the cells will have a width of 2h . Within a vertical distance of nc3 x (4h) , the cells will have a width of 4h . Etc…
box: refines inside the convex hull defined by the xy[z] locations. Consider a tree mesh whose smallest cell size has a width of h. And octree_levels = [nc1, nc2, nc3, …] . Within the convex hull defined by xyz , the smallest cell size is used. Within a distance of nc2 x (2h) from that convex hull, the cells will have a width of 2h . Within a distance of nc3 x (4h) , the cells will have a width of 4h . Etc…
Deprecated since version 0.9.0: refine_tree_xyz will be removed in a future version of discretize. It is replaced by discretize.TreeMesh.refine_surface, discretize.TreeMesh.refine_bounding_box, and discretize.TreeMesh.refine_points, to separate the calling convetions, and improve the individual documentation. Those methods are more explicit about which levels of the TreeMesh you are refining, and provide more flexibility for padding cells in each dimension.
- Parameters:
- mesh
discretize.TreeMesh The tree mesh object to be refined
- xyz
numpy.ndarray 2D array of points (n, dim)
- method{‘radial’, ‘surface’, ‘box’}
Method used to refine the mesh based on xyz locations.
radial: Based on radial distance xy[z] and cell centers
surface: Refines downward from a triangulated surface
box: Inside limits defined by outer xy[z] locations
- octree_levels
listofint,optional Minimum number of cells around points in each k octree level starting from the smallest cells size; i.e. [nc(k), nc(k-1), …] . Note that you can set entries to 0; e.g. you don’t want to discretize using the smallest cell size.
- octree_levels_padding
listofint,optional Padding cells added to extend the region of refinement at each level. Used for method = surface and box. Has the form [nc(k), nc(k-1), …]
- finalizebool,
optional Finalize the tree mesh.
- min_level
int,optional Sets the largest cell size allowed in the mesh. The default (0), allows the largest cell size to be used.
- max_distance
float Maximum refinement distance from xy[z] locations. Used if method = “surface” to reduce interpolation distance
- mesh
- Returns:
discretize.TreeMeshThe refined tree mesh
See also
discretize.TreeMesh.refine_surfaceRecommended to use instead of this function for the surface option.
discretize.TreeMesh.refine_bounding_boxRecommended to use instead of this function for the box option.
discretize.TreeMesh.refine_pointsRecommended to use instead of this function for the radial option.
Examples
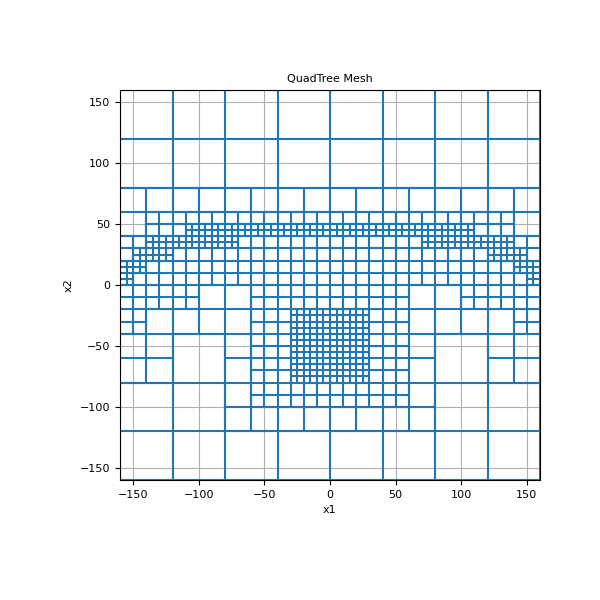
Here we use the refine_tree_xyz function refine a tree mesh based on topography as well as a cluster of points.
>>> from discretize import TreeMesh >>> from discretize.utils import mkvc, refine_tree_xyz >>> import matplotlib.pyplot as plt >>> import numpy as np
>>> dx = 5 # minimum cell width (base mesh cell width) in x >>> dy = 5 # minimum cell width (base mesh cell width) in y >>> x_length = 300.0 # domain width in x >>> y_length = 300.0 # domain width in y
Compute number of base mesh cells required in x and y
>>> nbcx = 2 ** int(np.round(np.log(x_length / dx) / np.log(2.0))) >>> nbcy = 2 ** int(np.round(np.log(y_length / dy) / np.log(2.0)))
Define the base mesh
>>> hx = [(dx, nbcx)] >>> hy = [(dy, nbcy)] >>> mesh = TreeMesh([hx, hy], x0="CC")
Refine surface topography
>>> xx = mesh.nodes_x >>> yy = -3 * np.exp((xx ** 2) / 100 ** 2) + 50.0 >>> pts = np.c_[mkvc(xx), mkvc(yy)] >>> mesh = refine_tree_xyz( ... mesh, pts, octree_levels=[2, 4], method="surface", finalize=False ... )
Refine mesh near points
>>> xx = np.array([-10.0, 10.0, 10.0, -10.0]) >>> yy = np.array([-40.0, -40.0, -60.0, -60.0]) >>> pts = np.c_[mkvc(xx), mkvc(yy)] >>> mesh = refine_tree_xyz( ... mesh, pts, octree_levels=[4, 2], method="radial", finalize=True ... )
Plot the mesh
>>> fig = plt.figure(figsize=(6, 6)) >>> ax = fig.add_subplot(111) >>> mesh.plot_grid(ax=ax) >>> ax.set_xbound(mesh.x0[0], mesh.x0[0] + np.sum(mesh.h[0])) >>> ax.set_ybound(mesh.x0[1], mesh.x0[1] + np.sum(mesh.h[1])) >>> ax.set_title("QuadTree Mesh") >>> plt.show()
(
Source code,png,pdf)