discretize.utils.make_property_tensor#
- discretize.utils.make_property_tensor(mesh, tensor)[source]#
Construct the physical property tensor.
For a given mesh, the input parameter tensor is a
numpy.ndarraydefining the constitutive relationship (e.g. Ohm’s law) between two discrete vector quantities \(\boldsymbol{j}\) and \(\boldsymbol{e}\) living at cell centers. The function make_property_tensor constructs the property tensor \(\boldsymbol{M}\) for the entire mesh such that:>>> j = M @ e
where the Cartesian components of the discrete vector for are organized according to:
>>> e = np.r_[ex, ey, ez] >>> j = np.r_[jx, jy, jz]
- Parameters:
- mesh
discretize.base.BaseMesh A mesh
- tensor
numpy.ndarrayorafloat Scalar: A float is entered.
Isotropic: A 1D numpy.ndarray with a property value for every cell.
Anisotropic: A (nCell, dim) numpy.ndarray where each row defines the diagonal-anisotropic property parameters for each cell. nParam = 2 for 2D meshes and nParam = 3 for 3D meshes.
Tensor: A (nCell, nParam) numpy.ndarray where each row defines the full anisotropic property parameters for each cell. nParam = 3 for 2D meshes and nParam = 6 for 3D meshes.
- mesh
- Returns:
- (
dim*n_cells,dim*n_cells)scipy.sparse.coo_matrix The property tensor.
- (
Notes
The relationship between a quantity and its response to external stimuli (e.g. Ohm’s law) in each cell can be defined by a scalar function \(\sigma\) in the isotropic case, or by a tensor \(\Sigma\) in the anisotropic case, i.e.:
\[\vec{j} = \sigma \vec{e} \;\;\;\;\;\; \textrm{or} \;\;\;\;\;\; \vec{j} = \Sigma \vec{e}\]where
\[\begin{split}\Sigma = \begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{xy} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{xz} & \sigma_{yz} & \sigma_{zz} \end{bmatrix}\end{split}\]Examples
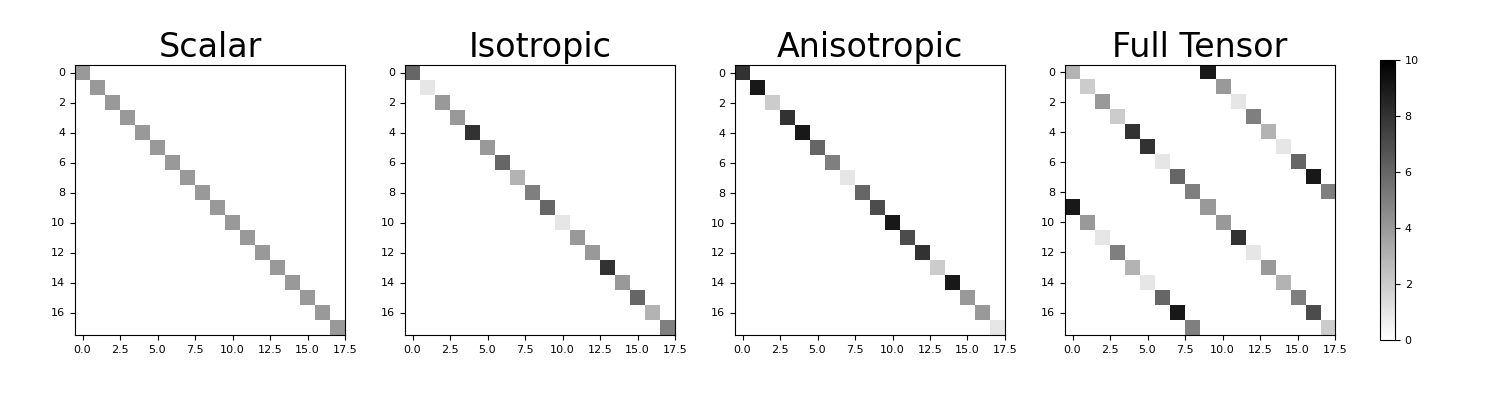
For the 4 classifications allowable (scalar, isotropic, anistropic and tensor), we construct and compare the property tensor on a small 2D mesh. For this example, note the following:
The dimensions for all property tensors are the same
All property tensors, except in the case of full anisotropy are diagonal sparse matrices
For the scalar case, the non-zero elements are equal
For the isotropic case, the non-zero elements repreat in order for the x, y (and z) components
For the anisotropic case (diagonal anisotropy), the non-zero elements do not repeat
For the tensor caes (full anisotropy), there are off-diagonal components
>>> from discretize.utils import make_property_tensor >>> from discretize import TensorMesh >>> import numpy as np >>> import matplotlib.pyplot as plt >>> import matplotlib as mpl >>> rng = np.random.default_rng(421)
Define a 2D tensor mesh
>>> h = [1., 1., 1.] >>> mesh = TensorMesh([h, h], origin='00')
Define a physical property for all cases (2D)
>>> sigma_scalar = 4. >>> sigma_isotropic = rng.integers(1, 10, mesh.nC) >>> sigma_anisotropic = rng.integers(1, 10, (mesh.nC, 2)) >>> sigma_tensor = rng.integers(1, 10, (mesh.nC, 3))
Construct the property tensor in each case
>>> M_scalar = make_property_tensor(mesh, sigma_scalar) >>> M_isotropic = make_property_tensor(mesh, sigma_isotropic) >>> M_anisotropic = make_property_tensor(mesh, sigma_anisotropic) >>> M_tensor = make_property_tensor(mesh, sigma_tensor)
Plot the property tensors.
>>> M_list = [M_scalar, M_isotropic, M_anisotropic, M_tensor] >>> case_list = ['Scalar', 'Isotropic', 'Anisotropic', 'Full Tensor'] >>> ax1 = 4*[None] >>> fig = plt.figure(figsize=(15, 4)) >>> for ii in range(0, 4): ... ax1[ii] = fig.add_axes([0.05+0.22*ii, 0.05, 0.18, 0.9]) ... ax1[ii].imshow( ... M_list[ii].todense(), interpolation='none', cmap='binary', vmax=10. ... ) ... ax1[ii].set_title(case_list[ii], fontsize=24) >>> ax2 = fig.add_axes([0.92, 0.15, 0.01, 0.7]) >>> norm = mpl.colors.Normalize(vmin=0., vmax=10.) >>> cbar = mpl.colorbar.ColorbarBase( ... ax2, norm=norm, orientation="vertical", cmap=mpl.cm.binary ... ) >>> plt.show()
(
Source code,png,pdf)