discretize.utils.inverse_2x2_block_diagonal

discretize.utils.inverse_2x2_block_diagonal(a11, a12, a21, a22, return_matrix=True, **kwargs)

Invert a set of 2x2 matricies from vectors containing their elements.

Parameters:

a11, a12, a21, a22(n_blocks) numpy.ndarray

All arguments a11, a12, a21, a22 are vectors which contain the corresponding element for all 2x2 matricies

return_matrixbool, optional

• True: Returns the sparse block 2x2 matrix M.

• False: Returns the vectors containing the elements of each matrix’ inverse.

Returns:

(2 * n_blocks, 2 * n_blocks) scipy.sparse.coo_matrix or list of (n_blocks) numpy.ndarray

If return_matrix = False, the function will return vectors b11, b12, b21, b22. If return_matrix = True, the function will return the block matrix M

Notes

The elements of a 2x2 matrix A are given by:

\[\begin{split}A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix}\end{split}\]

For a set of 2x2 matricies, the elements may be stored in a set of 4 distinct vectors \(\mathbf{a_{11}}\), \(\mathbf{a_{12}}\), \(\mathbf{a_{21}}\) and \(\mathbf{a_{22}}\). For each matrix, inverse_2x2_block_diagonal ouputs the vectors containing the elements of each matrix’ inverse; i.e. \(\mathbf{b_{11}}\), \(\mathbf{b_{12}}\), \(\mathbf{b_{21}}\) and \(\mathbf{b_{22}}\) where:

\[\begin{split}A^{-1} = B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{bmatrix}\end{split}\]

For special applications, we may want to output the elements of the inverses of the matricies as a 2x2 block matrix of the form:

\[\begin{split}M = \begin{bmatrix} D_{11} & D_{12} \\ D_{21} & D_{22} \end{bmatrix}\end{split}\]

where \(D_{ij}\) are diagonal matrices whose non-zero elements are defined by vector \(\mathbf{b_{ij}}\). Where n is the number of matricies, the block matrix is sparse with dimensions (2n, 2n).

Examples

Here, we define four 2x2 matricies and reorganize their elements into 4 vectors a11, a12, a21 and a22. We then examine the outputs of the function inverse_2x2_block_diagonal when the argument return_matrix is set to both True and False.

>>> from discretize.utils import inverse_2x2_block_diagonal
>>> import numpy as np
>>> import matplotlib.pyplot as plt

Define four 3x3 matricies, and organize their elements into four vectors

>>> A1 = np.random.uniform(1, 10, (2, 2))
>>> A2 = np.random.uniform(1, 10, (2, 2))
>>> A3 = np.random.uniform(1, 10, (2, 2))
>>> A4 = np.random.uniform(1, 10, (2, 2))
>>> [[a11, a12], [a21, a22]] = np.stack([A1, A2, A3, A4], axis=-1)

Return the elements of their inverse and validate

>>> b11, b12, b21, b22 = inverse_2x2_block_diagonal(
...     a11, a12, a21, a22, return_matrix=False
... )
>>> Bs = np.stack([[b11, b12],[b21, b22]])
>>> B1, B2, B3, B4 = Bs.transpose((2, 0, 1))

>>> np.linalg.inv(A1)
array([[ 0.34507439, -0.4831833 ],
       [-0.24286626,  0.57531461]])
>>> B1
array([[ 0.34507439, -0.4831833 ],
       [-0.24286626,  0.57531461]])

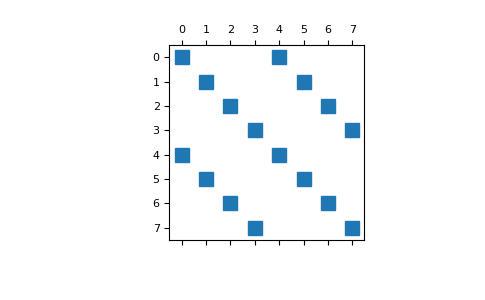
Plot the sparse block matrix containing elements of the inverses

>>> M = inverse_2x2_block_diagonal(
...     a11, a12, a21, a22
... )
>>> plt.spy(M)
>>> plt.show()

(Source code, png, pdf)