discretize.CylindricalMesh.face_y_divergence

property CylindricalMesh.face_y_divergence

Y-derivative operator (y-faces to cell-centres).

This property constructs a 2nd order y-derivative operator which maps from y-faces to cell centers. The operator is a sparse matrix \(\mathbf{D_y}\) that can be applied as a matrix-vector product to a discrete scalar quantity \(\boldsymbol{\phi}\) that lives on y-faces; i.e.:

dphi_dy = Dy @ phi

For a discrete vector whose y-component lives on y-faces, this operator can also be used to compute the contribution of the y-component toward the divergence.

Returns:

(n_cells, n_faces_y) scipy.sparse.csr_matrix

The numerical y-derivative operator from y-faces to cell centers

Examples

Below, we demonstrate 1) how to apply the face-y divergence operator, and 2) the mapping of the face-y divergence operator and its sparsity. Our example is carried out on a 2D mesh but it can be done equivalently for a 3D mesh.

We start by importing the necessary packages and modules.

>>> from discretize import TensorMesh
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import matplotlib as mpl

For a discrete scalar quantity \(\boldsymbol{\phi}\) defined on the y-faces, we take the y-derivative by constructing the face-y divergence operator and multiplying as a matrix-vector product.

>>> h = np.ones(40)
>>> mesh = TensorMesh([h, h], "CC")

Create a discrete quantity on x-faces

>>> faces_y = mesh.faces_y
>>> phi = np.exp(-(faces_y[:, 1] ** 2) / 8** 2)

Construct the y-divergence operator and apply to vector

>>> Dy = mesh.face_y_divergence
>>> dphi_dy = Dy @ phi

Plot original function and the y-divergence

>>> fig = plt.figure(figsize=(13, 6))
>>> ax1 = fig.add_subplot(121)
>>> w = np.r_[np.ones(mesh.nFx), phi]  # Need vector on all faces for image plot
>>> mesh.plot_image(w, ax=ax1, v_type="Fy")
>>> ax1.set_title("Scalar on y-faces", fontsize=14)
>>> ax2 = fig.add_subplot(122)
>>> mesh.plot_image(dphi_dy, ax=ax2)
>>> ax2.set_yticks([])
>>> ax2.set_ylabel("")
>>> ax2.set_title("Y-derivative at cell center", fontsize=14)
>>> plt.show()

(Source code, png, pdf)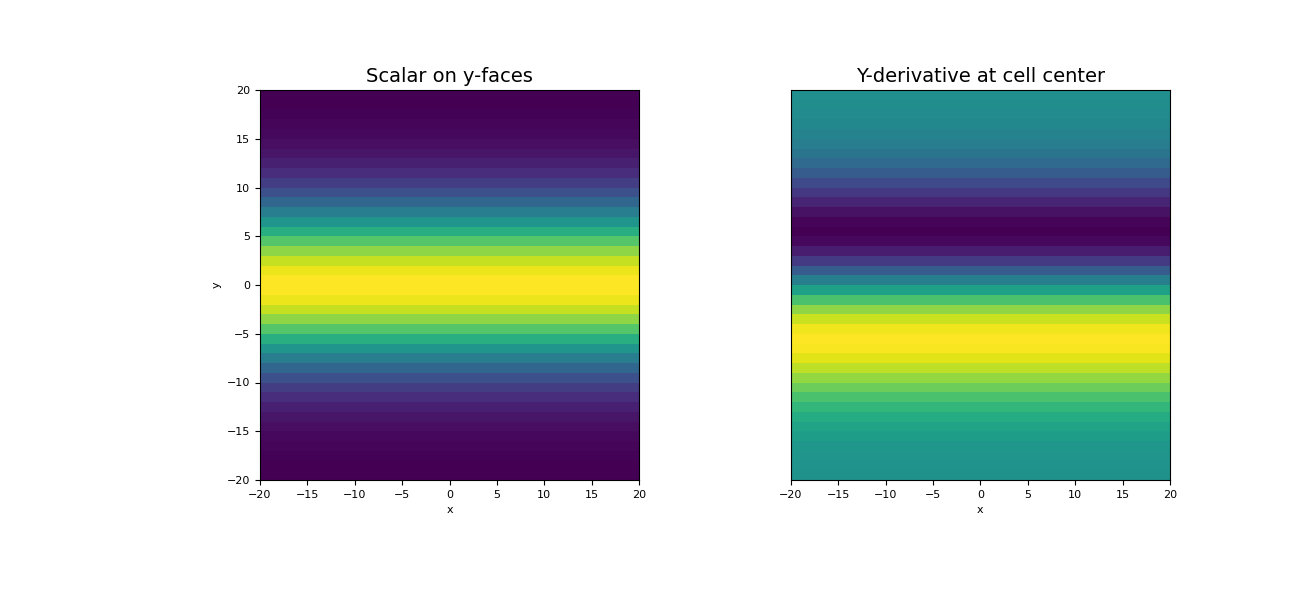

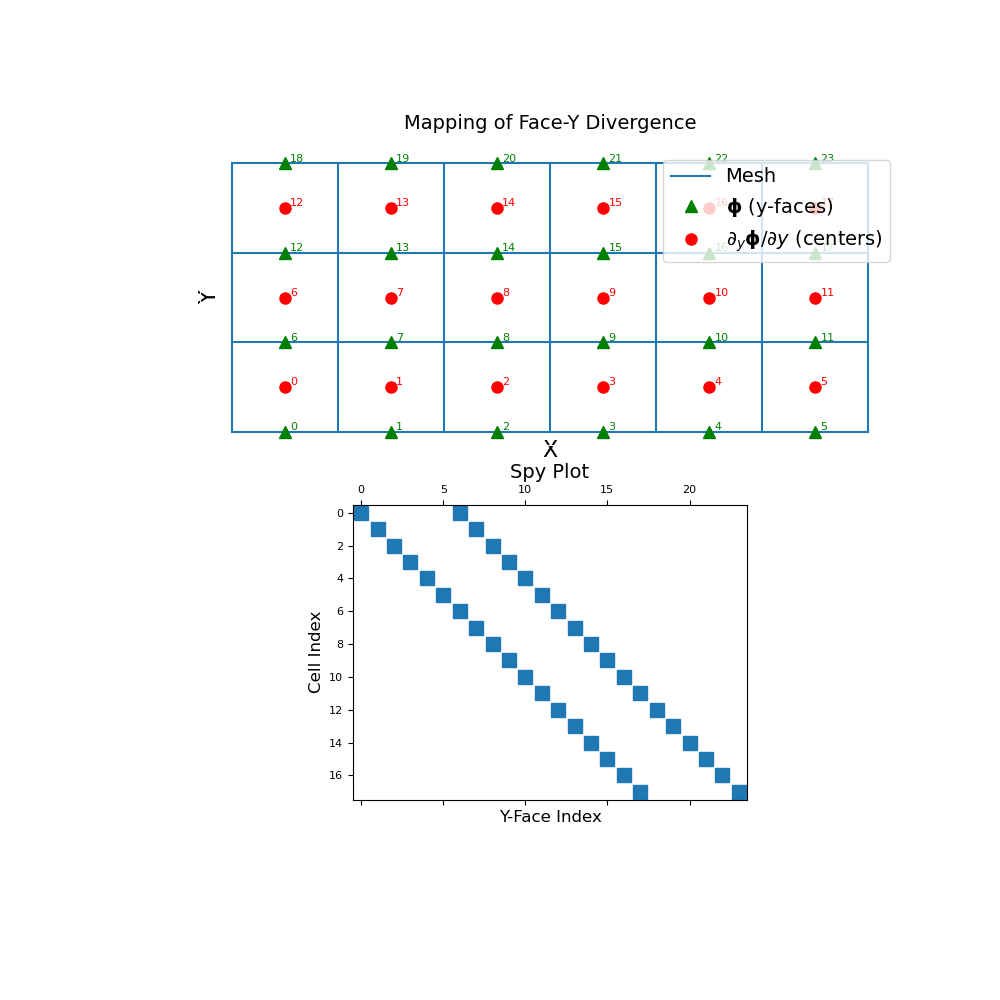
The discrete y-face divergence operator is a sparse matrix that maps from y-faces to cell centers. To demonstrate this, we construct a small 2D mesh. We then show the ordering of the elements in the original discrete quantity \(\boldsymbol{\phi}\) and its y-derivative \(\partial \boldsymbol{\phi}/ \partial y\) as well as a spy plot.

>>> mesh = TensorMesh([[(1, 6)], [(1, 3)]])
>>> fig = plt.figure(figsize=(10, 10))
>>> ax1 = fig.add_subplot(211)
>>> mesh.plot_grid(ax=ax1)
>>> ax1.plot(
...     mesh.faces_y[:, 0], mesh.faces_y[:, 1], "g^", markersize=8
... )
>>> for ii, loc in zip(range(mesh.nFy), mesh.faces_y):
...     ax1.text(loc[0]+0.05, loc[1]+0.02, "{0:d}".format(ii), color="g")
>>> ax1.plot(
...     mesh.cell_centers[:, 0], mesh.cell_centers[:, 1], "ro", markersize=8
... )
>>> for ii, loc in zip(range(mesh.nC), mesh.cell_centers):
...     ax1.text(loc[0]+0.05, loc[1]+0.02, "{0:d}".format(ii), color="r")
>>> ax1.set_xticks([])
>>> ax1.set_yticks([])
>>> ax1.spines['bottom'].set_color('white')
>>> ax1.spines['top'].set_color('white')
>>> ax1.spines['left'].set_color('white')
>>> ax1.spines['right'].set_color('white')
>>> ax1.set_xlabel('X', fontsize=16, labelpad=-5)
>>> ax1.set_ylabel('Y', fontsize=16, labelpad=-15)
>>> ax1.set_title("Mapping of Face-Y Divergence", fontsize=14, pad=15)
>>> ax1.legend(
...     ['Mesh',r'$\mathbf{\phi}$ (y-faces)',r'$\partial_y \mathbf{\phi}/\partial y$ (centers)'],
...     loc='upper right', fontsize=14
... )
>>> ax2 = fig.add_subplot(212)
>>> ax2.spy(mesh.face_y_divergence)
>>> ax2.set_title("Spy Plot", fontsize=14, pad=5)
>>> ax2.set_ylabel("Cell Index", fontsize=12)
>>> ax2.set_xlabel("Y-Face Index", fontsize=12)
>>> plt.show()

(png, pdf)