discretize.CylindricalMesh.get_edge_inner_product_surface#
- CylindricalMesh.get_edge_inner_product_surface(model=None, invert_model=False, invert_matrix=False, **kwargs)[source]#
Generate the edge inner product surface matrix or its inverse.
This method generates the inner product surface matrix (or its inverse) when discrete variables are defined on mesh edges. It is also capable of constructing the inner product surface matrix when diagnostic properties (e.g. conductance) are defined on mesh faces. For a comprehensive description of the inner product surface matrices that can be constructed with get_edge_inner_product_surface, see Notes.
- Parameters:
- model
Noneornumpy.ndarray Parameters defining the diagnostic properties for every face in the mesh. Inner product surface matrices can be constructed for the following cases:
None : returns the basic inner product surface matrix
(n_faces)
numpy.ndarray: returns inner product surface matrix for an isotropic model. The array contains a scalar diagnostic property value for each face.
- invert_modelbool,
optional The inverse of model is used as the diagnostic property.
- invert_matrixbool,
optional Returns the inverse of the inner product surface matrix. The inverse not implemented for full tensor properties.
- model
- Returns:
- (
n_edges,n_edges)scipy.sparse.csr_matrix inner product surface matrix
- (
Notes
For continuous vector quantities \(\vec{u}\) and \(\vec{w}\), and scalar physical property distribution \(\sigma\), we define the following inner product:
\[\langle \vec{u}, \sigma \vec{w} \rangle = \int_\Omega \, \vec{u} \cdot \sigma \vec{v} \, dv\]If the material property is distributed over a set of surfaces \(S_i\) with thickness \(h\), we can define a diagnostic property value \(\tau = \sigma h\). And the inner-product can be approximated by a set of surface integrals as follows:
\[\langle \vec{u}, \sigma \vec{w} \rangle = \sum_i \int_{S_i} \, \vec{u} \cdot \tau \vec{v} \, da\]Let \(\vec{u}\) and \(\vec{w}\) have discrete representations \(\mathbf{u}\) and \(\mathbf{w}\) that live on the edges. Assuming the contribution of vector components normal to the surface are negligible compared to tangential components, get_edge_inner_product_suface constructs the inner product matrix \(\mathbf{M_\tau}\) (or its inverse \(\mathbf{M_\tau^{-1}}\)) such that:
\[\sum_i \int_{S_i} \, \vec{u} \cdot \tau \vec{v} \, da \approx \sum_i \int_{S_i} \, \vec{u}_\parallel \cdot \tau \vec{v}_\parallel \, da = \mathbf{u^T \, M_\tau \, w}\]where the diagnostic properties on mesh faces (i.e. the model) are stored within an array of the form:
\[\begin{split}\boldsymbol{\tau} = \begin{bmatrix} \boldsymbol{\tau_x} \\ \boldsymbol{\tau_y} \\ \boldsymbol{\tau_z} \end{bmatrix}\end{split}\]Examples
Here we provide an example of edge inner product surface matrix. For simplicity, we will work on a 2 x 2 x 2 tensor mesh. As seen below, we begin by constructing and imaging the basic edge inner product surface matrix.
>>> from discretize import TensorMesh >>> import matplotlib.pyplot as plt >>> import numpy as np >>> import matplotlib as mpl
>>> h = np.ones(2) >>> mesh = TensorMesh([h, h, h]) >>> Me = mesh.get_edge_inner_product_surface()
>>> fig = plt.figure(figsize=(6, 6)) >>> ax = fig.add_subplot(111) >>> ax.imshow(Me.todense()) >>> ax.set_title('Basic Edge Inner Product Surface Matrix', fontsize=18) >>> plt.show()
(
Source code,png,pdf)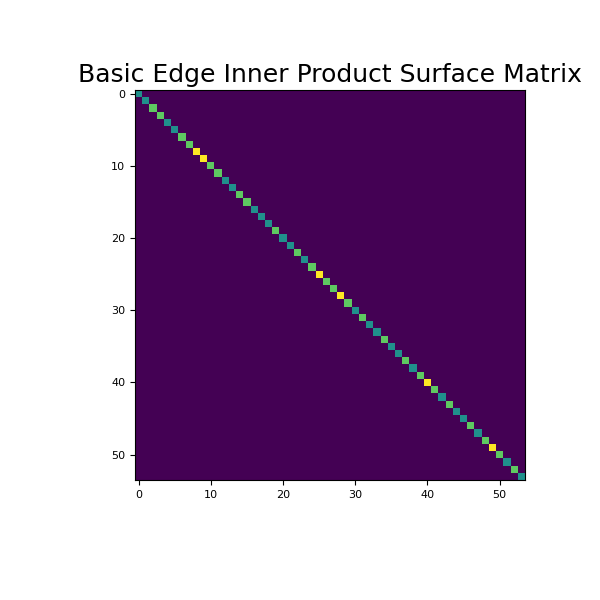
Next, we consider the case where the physical properties are defined by diagnostic properties on mesh faces. For the isotropic case, we show the physical property tensor for a single cell.
Define the diagnostic property values for x, y and z faces.
>>> tau_x, tau_y, tau_z = 3, 2, 1
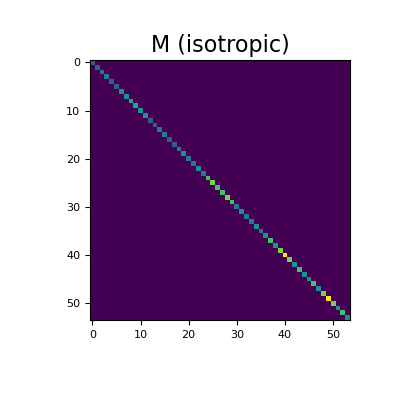
Here construct and image the edge inner product surface matrix for the isotropic case. Spy plots are used to demonstrate the sparsity of the inner product surface matrices.
>>> tau = np.r_[ >>> tau_x * np.ones(mesh.n_faces_x), >>> tau_y * np.ones(mesh.n_faces_y), >>> tau_z * np.ones(mesh.n_faces_z) >>> ] >>> M = mesh.get_edge_inner_product_surface(tau)
Then plot the sparse representation,
>>> fig = plt.figure(figsize=(4, 4)) >>> ax1 = fig.add_subplot(111) >>> ax1.imshow(M.todense()) >>> ax1.set_title("M (isotropic)", fontsize=16) >>> plt.show()