discretize.CylindricalMesh.face_y_divergence#
- property CylindricalMesh.face_y_divergence#
Y-derivative operator (y-faces to cell-centres).
This property constructs a 2nd order y-derivative operator which maps from y-faces to cell centers. The operator is a sparse matrix \(\mathbf{D_y}\) that can be applied as a matrix-vector product to a discrete scalar quantity \(\boldsymbol{\phi}\) that lives on y-faces; i.e.:
dphi_dy = Dy @ phi
For a discrete vector whose y-component lives on y-faces, this operator can also be used to compute the contribution of the y-component toward the divergence.
- Returns:
- (
n_cells,n_faces_y)scipy.sparse.csr_matrix The numerical y-derivative operator from y-faces to cell centers
- (
Examples
Below, we demonstrate 1) how to apply the face-y divergence operator, and 2) the mapping of the face-y divergence operator and its sparsity. Our example is carried out on a 2D mesh but it can be done equivalently for a 3D mesh.
We start by importing the necessary packages and modules.
>>> from discretize import TensorMesh >>> import numpy as np >>> import matplotlib.pyplot as plt >>> import matplotlib as mpl
For a discrete scalar quantity \(\boldsymbol{\phi}\) defined on the y-faces, we take the y-derivative by constructing the face-y divergence operator and multiplying as a matrix-vector product.
>>> h = np.ones(40) >>> mesh = TensorMesh([h, h], "CC")
Create a discrete quantity on x-faces
>>> faces_y = mesh.faces_y >>> phi = np.exp(-(faces_y[:, 1] ** 2) / 8** 2)
Construct the y-divergence operator and apply to vector
>>> Dy = mesh.face_y_divergence >>> dphi_dy = Dy @ phi
Plot original function and the y-divergence
>>> fig = plt.figure(figsize=(13, 6)) >>> ax1 = fig.add_subplot(121) >>> w = np.r_[np.ones(mesh.nFx), phi] # Need vector on all faces for image plot >>> mesh.plot_image(w, ax=ax1, v_type="Fy") >>> ax1.set_title("Scalar on y-faces", fontsize=14) >>> ax2 = fig.add_subplot(122) >>> mesh.plot_image(dphi_dy, ax=ax2) >>> ax2.set_yticks([]) >>> ax2.set_ylabel("") >>> ax2.set_title("Y-derivative at cell center", fontsize=14) >>> plt.show()
(
Source code,png,pdf)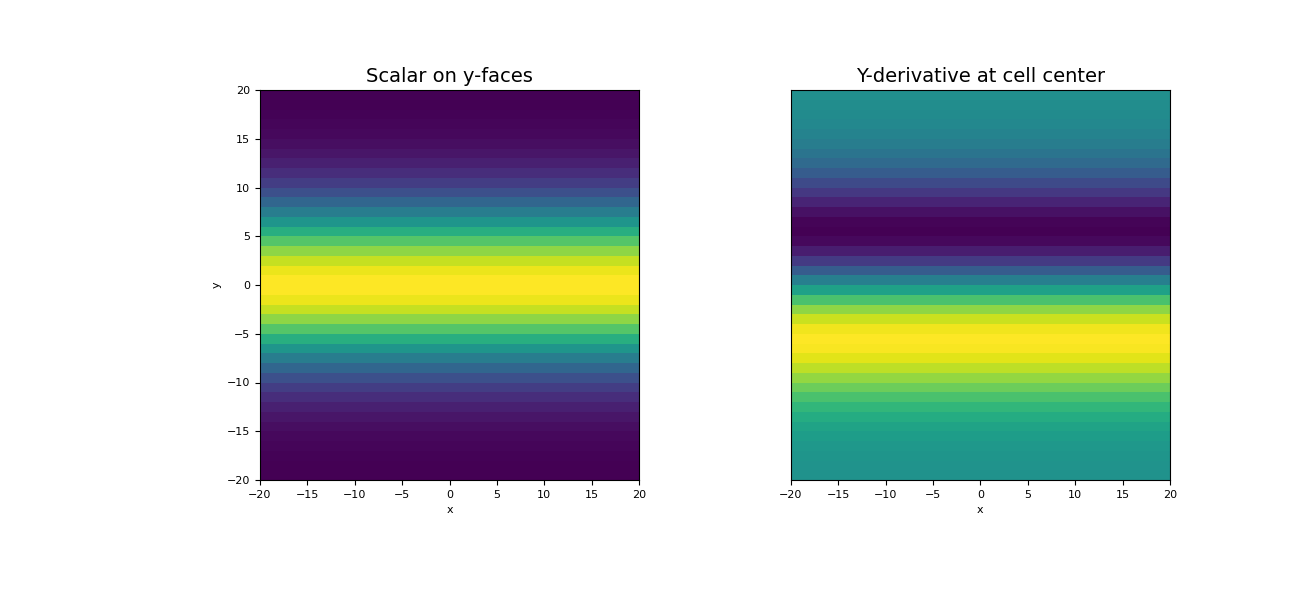
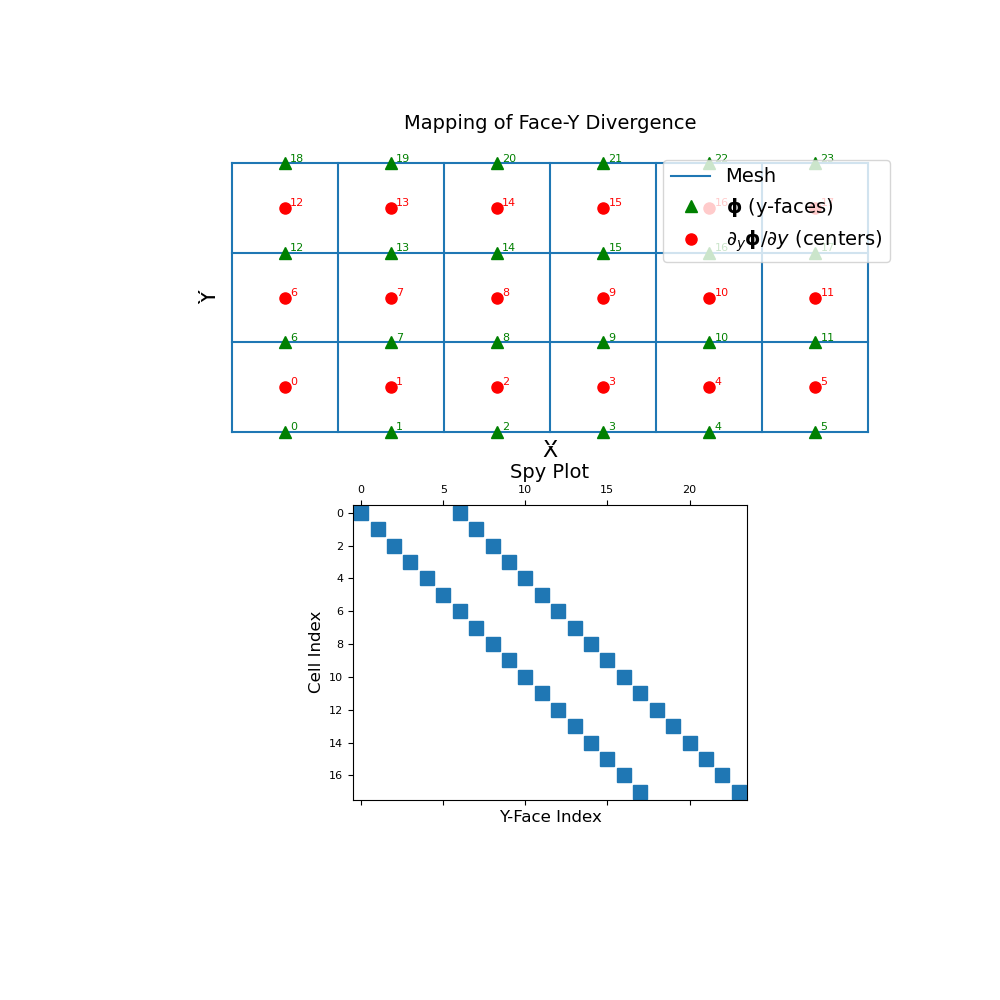
The discrete y-face divergence operator is a sparse matrix that maps from y-faces to cell centers. To demonstrate this, we construct a small 2D mesh. We then show the ordering of the elements in the original discrete quantity \(\boldsymbol{\phi}\) and its y-derivative \(\partial \boldsymbol{\phi}/ \partial y\) as well as a spy plot.
>>> mesh = TensorMesh([[(1, 6)], [(1, 3)]]) >>> fig = plt.figure(figsize=(10, 10)) >>> ax1 = fig.add_subplot(211) >>> mesh.plot_grid(ax=ax1) >>> ax1.plot( ... mesh.faces_y[:, 0], mesh.faces_y[:, 1], "g^", markersize=8 ... ) >>> for ii, loc in zip(range(mesh.nFy), mesh.faces_y): ... ax1.text(loc[0]+0.05, loc[1]+0.02, "{0:d}".format(ii), color="g") >>> ax1.plot( ... mesh.cell_centers[:, 0], mesh.cell_centers[:, 1], "ro", markersize=8 ... ) >>> for ii, loc in zip(range(mesh.nC), mesh.cell_centers): ... ax1.text(loc[0]+0.05, loc[1]+0.02, "{0:d}".format(ii), color="r") >>> ax1.set_xticks([]) >>> ax1.set_yticks([]) >>> ax1.spines['bottom'].set_color('white') >>> ax1.spines['top'].set_color('white') >>> ax1.spines['left'].set_color('white') >>> ax1.spines['right'].set_color('white') >>> ax1.set_xlabel('X', fontsize=16, labelpad=-5) >>> ax1.set_ylabel('Y', fontsize=16, labelpad=-15) >>> ax1.set_title("Mapping of Face-Y Divergence", fontsize=14, pad=15) >>> ax1.legend( ... ['Mesh','$\mathbf{\phi}$ (y-faces)','$\partial_y \mathbf{\phi}/\partial y$ (centers)'], ... loc='upper right', fontsize=14 ... ) >>> ax2 = fig.add_subplot(212) >>> ax2.spy(mesh.face_y_divergence) >>> ax2.set_title("Spy Plot", fontsize=14, pad=5) >>> ax2.set_ylabel("Cell Index", fontsize=12) >>> ax2.set_xlabel("Y-Face Index", fontsize=12) >>> plt.show()