discretize.CurvilinearMesh.average_face_to_cell_vector#
- property CurvilinearMesh.average_face_to_cell_vector#
Averaging operator from faces to cell centers (vector quantities).
This property constructs the averaging operator that independently maps the Cartesian components of vector quantities from faces to cell centers. This averaging operators is used when a discrete vector quantity defined on mesh faces must be approximated at cell centers. Once constructed, the operator is stored permanently as a property of the mesh.
Be aware that the Cartesian components of the original vector are defined on their respective faces; e.g. the x-component lives on x-faces. However, the x, y and z components are being averaged separately to cell centers. The operation is implemented as a matrix vector product, i.e.:
u_c = Afc @ u_f
- Returns:
- (
dim*n_cells,n_faces)scipy.sparse.csr_matrix The vector averaging operator from faces to cell centers. Since we are averaging a vector quantity to cell centers, the first dimension of the operator is the mesh dimension times the number of cells.
- (
Notes
Let \(\mathbf{u_f}\) be the discrete representation of a vector quantity whose Cartesian components are defined on their respective faces; e.g. \(u_x\) is defined on x-faces. average_face_to_cell_vector constructs a discrete linear operator \(\mathbf{A_{fc}}\) that projects each Cartesian component of \(\mathbf{u_f}\) independently to cell centers, i.e.:
\[\mathbf{u_c} = \mathbf{A_{fc}} \, \mathbf{u_f}\]where \(\mathbf{u_c}\) is a discrete vector quantity whose Cartesian components defined at the cell centers and organized into a 1D array of the form np.r_[ux, uy, uz]. For each cell, and for each Cartesian component, we are simply taking the average of the values defined on the cell’s corresponding faces and placing the result at the cell’s center.
Examples
Here we compute the values of a vector function discretized to the mesh faces. We then create an averaging operator to approximate the function at cell centers.
We start by importing the necessary packages and defining a mesh.
>>> from discretize import TensorMesh >>> import numpy as np >>> import matplotlib.pyplot as plt
>>> h = 0.5 * np.ones(40) >>> mesh = TensorMesh([h, h], x0="CC")
Then we create a discrete vector on mesh faces
>>> faces_x = mesh.faces_x >>> faces_y = mesh.faces_y >>> u_fx = -(faces_x[:, 1] / np.sqrt(np.sum(faces_x ** 2, axis=1))) * np.exp( >>> -(faces_x[:, 0] ** 2 + faces_x[:, 1] ** 2) / 6 ** 2 >>> ) >>> u_fy = (faces_y[:, 0] / np.sqrt(np.sum(faces_y ** 2, axis=1))) * np.exp( >>> -(faces_y[:, 0] ** 2 + faces_y[:, 1] ** 2) / 6 ** 2 >>> ) >>> u_f = np.r_[u_fx, u_fy]
Next, we construct the averaging operator and apply it to the discrete vector quantity to approximate the value at cell centers.
>>> Afc = mesh.average_face_to_cell_vector >>> u_c = Afc @ u_f
And finally, plot the results:
>>> fig = plt.figure(figsize=(11, 5)) >>> ax1 = fig.add_subplot(121) >>> mesh.plot_image(u_f, ax=ax1, v_type="F", view='vec') >>> ax1.set_title("Variable at faces", fontsize=16) >>> ax2 = fig.add_subplot(122) >>> mesh.plot_image(u_c, ax=ax2, v_type="CCv", view='vec') >>> ax2.set_title("Averaged to cell centers", fontsize=16) >>> plt.show()
(
Source code,png,pdf)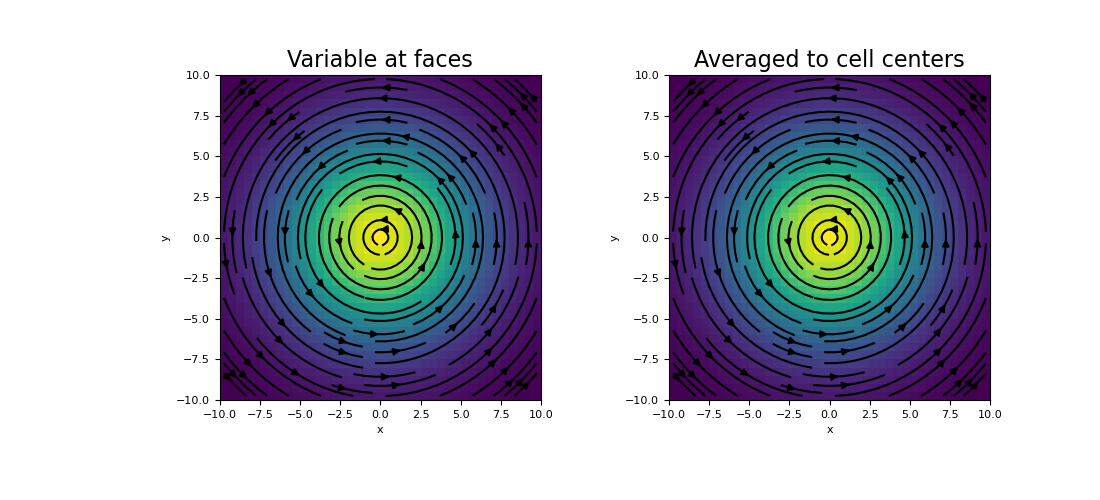
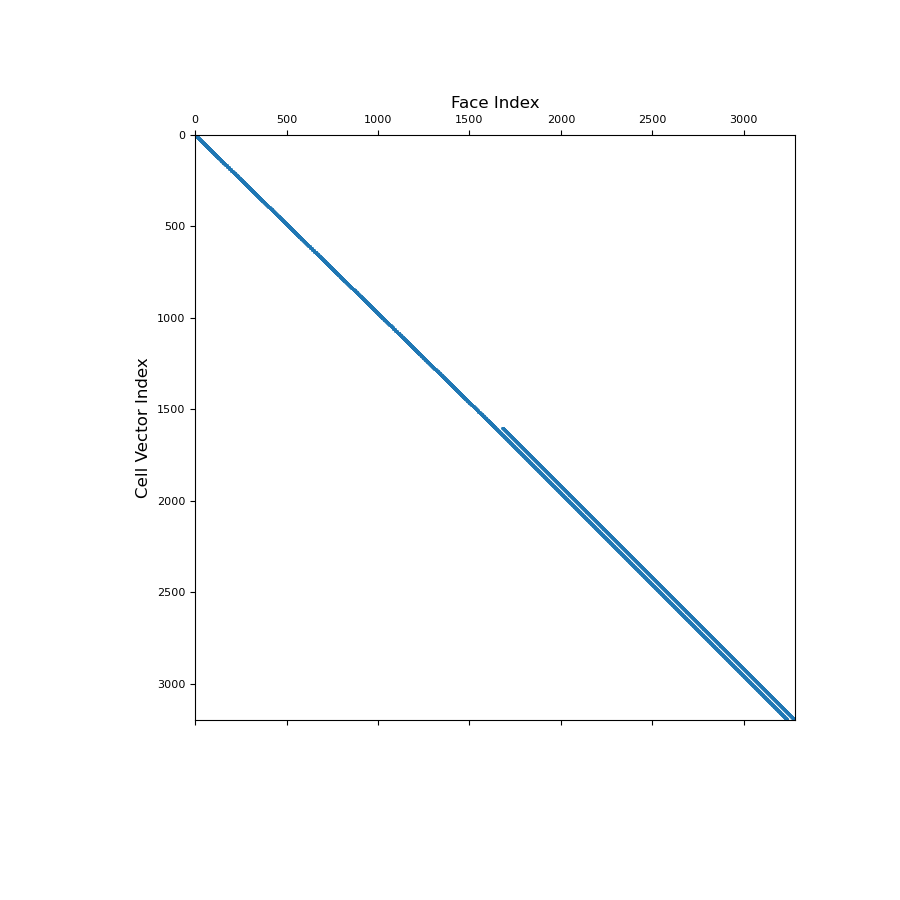
Below, we show a spy plot illustrating the sparsity and mapping of the operator
>>> fig = plt.figure(figsize=(9, 9)) >>> ax1 = fig.add_subplot(111) >>> ax1.spy(Afc, ms=1) >>> ax1.set_title("Face Index", fontsize=12, pad=5) >>> ax1.set_ylabel("Cell Vector Index", fontsize=12) >>> plt.show()