discretize.operators.DiffOperators.stencil_cell_gradient#
- property DiffOperators.stencil_cell_gradient#
Stencil for cell gradient operator (cell centers to faces).
This property constructs a differencing operator that acts on cell centered quantities. The operator takes the difference between the values at adjacent cell centers along each axis direction, and places the result on the shared face; e.g. differences along the x-axis are mapped to x-faces. The operator is a sparse matrix \(\mathbf{G}\) that can be applied as a matrix-vector product to a cell centered quantity \(\boldsymbol{\phi}\), i.e.:
diff_phi = G @ phi
By default, the operator assumes zero-Neumann boundary conditions on the scalar quantity. Before calling stencil_cell_gradient however, the user can set a mix of zero Dirichlet and zero Neumann boundary conditions using
set_cell_gradient_BC. When stencil_cell_gradient is called, the boundary conditions are enforced for the differencing operator. Once constructed, the operator is stored as a property of the mesh.- Returns:
- (
n_faces,n_cells)scipy.sparse.csr_matrix The stencil for the cell gradient
- (
Examples
Below, we demonstrate how to set boundary conditions for the cell gradient stencil, construct the cell gradient stencil and apply it to a discrete scalar quantity. The mapping of the cell gradient operator and its sparsity is also illustrated. Our example is carried out on a 2D mesh but it can be done equivalently for a 3D mesh.
We start by importing the necessary packages and modules.
>>> from discretize import TensorMesh >>> import numpy as np >>> import matplotlib.pyplot as plt >>> import matplotlib as mpl
We then construct a mesh and define a scalar function at cell centers. In this case, the scalar represents some block within a homogeneous medium.
Create a uniform grid
>>> h = np.ones(40) >>> mesh = TensorMesh([h, h], "CC")
Create a discrete scalar at cell centers
>>> centers = mesh.cell_centers >>> phi = np.zeros(mesh.nC) >>> k = (np.abs(mesh.cell_centers[:, 0]) < 10.) & (np.abs(mesh.cell_centers[:, 1]) < 10.) >>> phi[k] = 1.
Before constructing the operator, we must define the boundary conditions; zero Neumann for our example. Once the operator is created, it is applied as a matrix-vector product.
>>> mesh.set_cell_gradient_BC(['neumann', 'neumann']) >>> G = mesh.stencil_cell_gradient >>> diff_phi = G @ phi
Now we plot the original scalar, and the differencing taken along the x and y axes.
>>> fig = plt.figure(figsize=(15, 4.5)) >>> ax1 = fig.add_subplot(131) >>> mesh.plot_image(phi, ax=ax1) >>> ax1.set_title("Scalar at cell centers", fontsize=14)
>>> ax2 = fig.add_subplot(132) >>> mesh.plot_image(diff_phi, ax=ax2, v_type="Fx") >>> ax2.set_yticks([]) >>> ax2.set_ylabel("") >>> ax2.set_title("Difference (x-axis)", fontsize=14)
>>> ax3 = fig.add_subplot(133) >>> mesh.plot_image(diff_phi, ax=ax3, v_type="Fy") >>> ax3.set_yticks([]) >>> ax3.set_ylabel("") >>> ax3.set_title("Difference (y-axis)", fontsize=14) >>> plt.show()
(
Source code,png,pdf)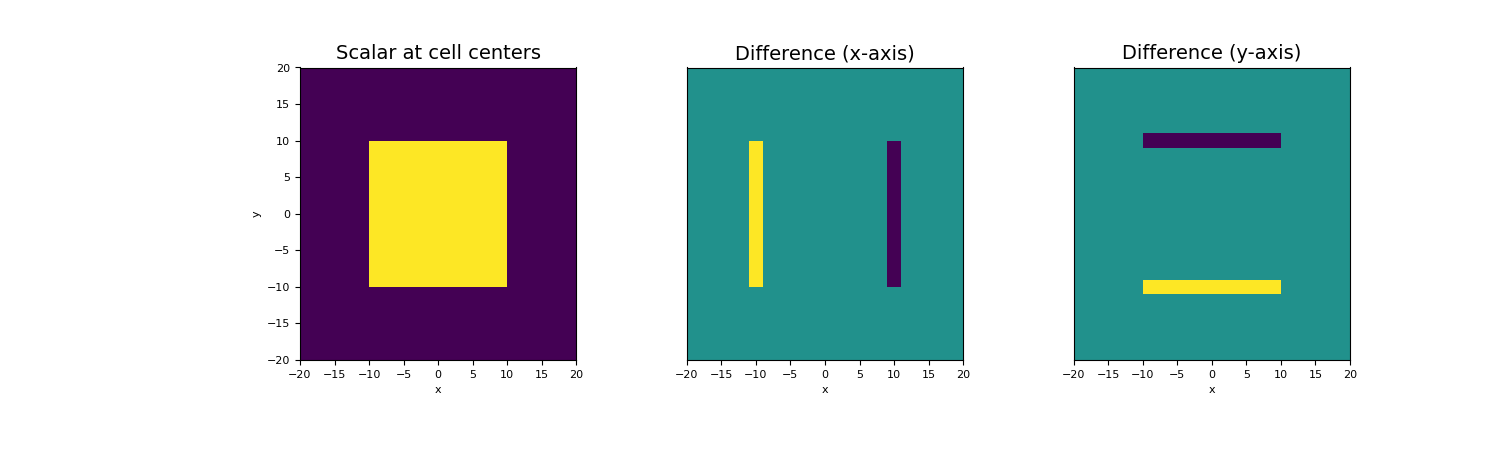
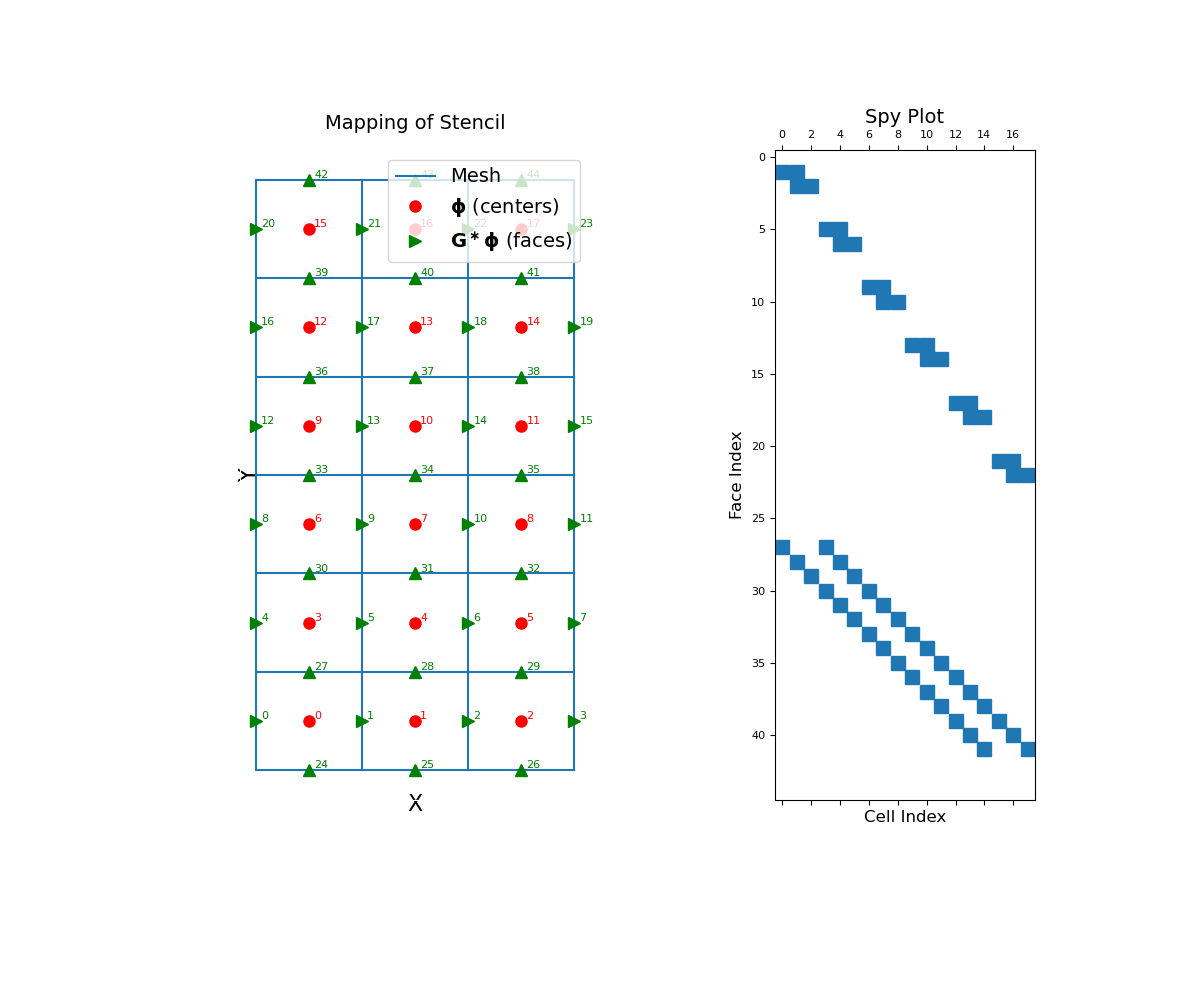
The cell gradient stencil is a sparse differencing matrix that maps from cell centers to faces. To demonstrate this, we construct a small 2D mesh. We then show the ordering of the elements and a spy plot.
>>> mesh = TensorMesh([[(1, 3)], [(1, 6)]]) >>> mesh.set_cell_gradient_BC('neumann')
>>> fig = plt.figure(figsize=(12, 10)) >>> ax1 = fig.add_subplot(121) >>> mesh.plot_grid(ax=ax1) >>> ax1.set_title("Mapping of Stencil", fontsize=14, pad=15) >>> ax1.plot(mesh.cell_centers[:, 0], mesh.cell_centers[:, 1], "ro", markersize=8) >>> for ii, loc in zip(range(mesh.nC), mesh.cell_centers): ... ax1.text(loc[0] + 0.05, loc[1] + 0.02, "{0:d}".format(ii), color="r") >>> ax1.plot(mesh.faces_x[:, 0], mesh.faces_x[:, 1], "g>", markersize=8) >>> for ii, loc in zip(range(mesh.nFx), mesh.faces_x): ... ax1.text(loc[0] + 0.05, loc[1] + 0.02, "{0:d}".format(ii), color="g") >>> ax1.plot(mesh.faces_y[:, 0], mesh.faces_y[:, 1], "g^", markersize=8) >>> for ii, loc in zip(range(mesh.nFy), mesh.faces_y): ... ax1.text(loc[0] + 0.05, loc[1] + 0.02, "{0:d}".format((ii + mesh.nFx)), color="g") >>> ax1.set_xticks([]) >>> ax1.set_yticks([]) >>> ax1.spines['bottom'].set_color('white') >>> ax1.spines['top'].set_color('white') >>> ax1.spines['left'].set_color('white') >>> ax1.spines['right'].set_color('white') >>> ax1.set_xlabel('X', fontsize=16, labelpad=-5) >>> ax1.set_ylabel('Y', fontsize=16, labelpad=-15) >>> ax1.legend( ... ['Mesh', r'$\mathbf{\phi}$ (centers)', r'$\mathbf{G^\ast \phi}$ (faces)'], ... loc='upper right', fontsize=14 ... )
>>> ax2 = fig.add_subplot(122) >>> ax2.spy(mesh.stencil_cell_gradient) >>> ax2.set_title("Spy Plot", fontsize=14, pad=5) >>> ax2.set_ylabel("Face Index", fontsize=12) >>> ax2.set_xlabel("Cell Index", fontsize=12) >>> plt.show()