discretize.mixins.InterfaceVTK#

- class discretize.mixins.InterfaceVTK[source]#
VTK interface for
discretizemeshes.Class enabling straight forward conversion between
discretizemeshes and their corresponding VTK or PyVista data objects. SinceInterfaceVTKis inherritted by theBaseMeshclass, this functionality can be called directly from anydiscretizemesh! Currently this functionality is implemented forCurvilinearMesh,TreeMeshanddiscretize.TensorMeshclasses; not implemented forCylindricalMesh.It should be noted that if your mesh is defined on a reference frame that is not the traditional <X,Y,Z> system with vectors of \((1,0,0)\), \((0,1,0)\), and \((0,0,1)\), then the mesh in VTK will be rotated so that it is plotted on the traditional reference frame; see examples below.
Methods
toVTK([models])Convert mesh (and models) to corresponding VTK or PyVista data object.
to_vtk([models])Convert mesh (and models) to corresponding VTK or PyVista data object.
writeVTK(file_name[, models, directory])Convert mesh (and models) to corresponding VTK or PyVista data object then writes to file.
write_vtk(file_name[, models, directory])Convert mesh (and models) to corresponding VTK or PyVista data object then writes to file.
Examples
The following are examples which use the VTK interface to convert discretize meshes to VTK data objects and write to VTK formatted files. In the first example example, a tensor mesh whose axes lie on the traditional reference frame is converted to a
pyvista.RectilinearGridobject.>>> import discretize >>> import numpy as np >>> h1 = np.linspace(.1, .5, 3) >>> h2 = np.linspace(.1, .5, 5) >>> h3 = np.linspace(.1, .8, 3) >>> mesh = discretize.TensorMesh([h1, h2, h3])
Get a VTK data object
>>> dataset = mesh.to_vtk()
Save this mesh to a VTK file
>>> mesh.write_vtk('sample_mesh')
Here, the reference frame of the mesh is rotated. In this case, conversion to VTK produces a
pyvista.StructuredGridobject.>>> axis_u = (1,-1,0) >>> axis_v = (-1,-1,0) >>> axis_w = (0,0,1) >>> mesh.orientation = np.array([ ... axis_u, ... axis_v, ... axis_w ... ])
Yield the rotated vtkStructuredGrid
>>> dataset_r = mesh.to_vtk()
or write it out to a VTK format
>>> mesh.write_vtk('sample_rotated')
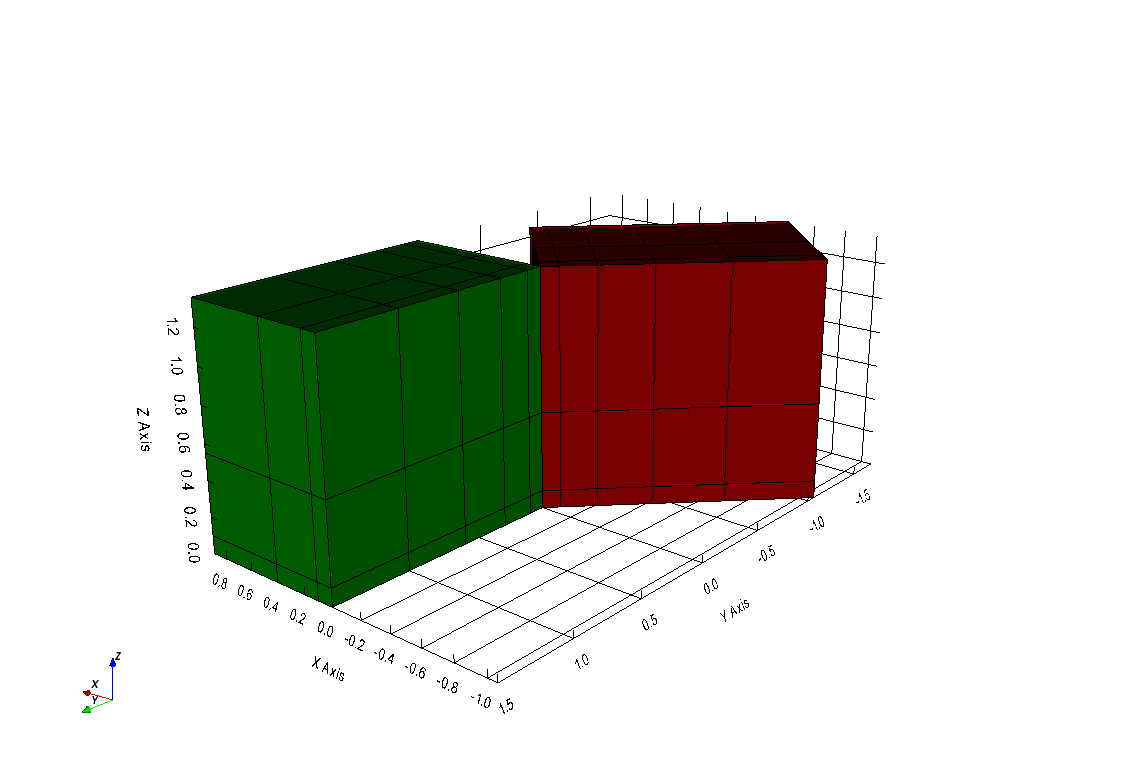
The two above code snippets produced a
pyvista.RectilinearGridand apyvista.StructuredGridrespecitvely. To demonstarte the difference, we have plotted the two datasets next to each other where the first mesh is in green and its data axes are parrallel to the traditional cartesian reference frame. The second, rotated mesh is shown in red and its data axes are rotated from the traditional Cartesian reference frame as specified by the orientation property.>>> import pyvista >>> pyvista.set_plot_theme('document')
>>> p = pyvista.BackgroundPlotter() >>> p.add_mesh(dataset, color='green', show_edges=True) >>> p.add_mesh(dataset_r, color='maroon', show_edges=True) >>> p.show_grid() >>> p.screenshot('vtk-rotated-example.png')