Note
Go to the end to download the full example code.
Plot Mirrored Cylindrically Symmetric Model#
Here, we demonstrate plotting a model on a cylindrically symmetric mesh with the plotting symmetric about x=0.
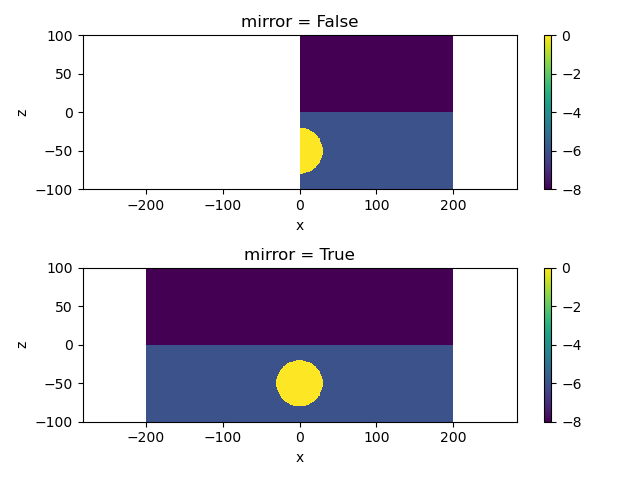
Ignoring fixed x limits to fulfill fixed data aspect with adjustable data limits.
Ignoring fixed x limits to fulfill fixed data aspect with adjustable data limits.
import numpy as np
import matplotlib.pyplot as plt
import discretize
def run(plotIt=True):
sig_halfspace = 1e-6
sig_sphere = 1e0
sig_air = 1e-8
sphere_z = -50.0
sphere_radius = 30.0
# x-direction
cs = 1
nc = np.ceil(2.5 * (-(sphere_z - sphere_radius)) / cs)
# define a mesh
mesh = discretize.CylindricalMesh([[(cs, nc)], 1, [(cs, nc)]], x0="00C")
# Put the model on the mesh
sigma = sig_air * np.ones(mesh.nC) # start with air cells
sigma[mesh.gridCC[:, 2] < 0.0] = sig_halfspace # cells below the earth
# indices of the sphere
sphere_ind = (
mesh.gridCC[:, 0] ** 2 + (mesh.gridCC[:, 2] - sphere_z) ** 2
) <= sphere_radius**2
sigma[sphere_ind] = sig_sphere # sphere
if not plotIt:
return
# Plot a cross section through the mesh
fig, ax = plt.subplots(2, 1)
# Set a nice colormap!
plt.set_cmap(plt.get_cmap("viridis"))
plt.colorbar(mesh.plot_image(np.log10(sigma), ax=ax[0])[0], ax=ax[0])
ax[0].set_title("mirror = False")
ax[0].axis("equal")
ax[0].set_xlim([-200.0, 200.0])
plt.colorbar(mesh.plot_image(np.log10(sigma), ax=ax[1], mirror=True)[0], ax=ax[1])
ax[1].set_title("mirror = True")
ax[1].axis("equal")
ax[1].set_xlim([-200.0, 200.0])
plt.tight_layout()
if __name__ == "__main__":
run()
plt.show()
Total running time of the script: (0 minutes 0.270 seconds)
