discretize.utils.face_info

discretize.utils.face_info(xyz, A, B, C, D, average=True, normalize_normals=True, **kwargs)

Return normal surface vectors and areas for a given set of faces.

Let xyz be an (n, 3) array denoting a set of vertex locations. Now let vertex locations a, b, c and d define a quadrilateral (regular or irregular) in 2D or 3D space. For this quadrilateral, we organize the vertices as follows:

CELL VERTICES:

      a -------Vab------- b
     /                   /
    /                   /
  Vda       (X)       Vbc
  /                   /
 /                   /
d -------Vcd------- c

where the normal vector (X) is pointing into the page. For a set of quadrilaterals whose vertices are indexed in arrays A, B, C and D , this function returns the normal surface vector(s) and the area for each quadrilateral.

At each vertex, there are 4 cross-products that can be used to compute the vector normal the surface defined by the quadrilateral. In 3D space however, the vertices indexed may not define a quadrilateral exactly and thus the normal vectors computed at each vertex might not be identical. In this case, you may choose output the normal vector at a, b, c and d or compute the average normal surface vector as follows:

\[\bf{n} = \frac{1}{4} \big ( \bf{v_{ab} \times v_{da}} + \bf{v_{bc} \times v_{ab}} + \bf{v_{cd} \times v_{bc}} + \bf{v_{da} \times v_{cd}} \big )\]

For computing the surface area, we assume the vertices define a quadrilateral.

Parameters:

xyz(n, 3) numpy.ndarray

The x,y, and z locations for all verticies

A(n_face) numpy.ndarray

Vector containing the indicies for the a vertex locations

B(n_face) numpy.ndarray

Vector containing the indicies for the b vertex locations

C(n_face) numpy.ndarray

Vector containing the indicies for the c vertex locations

D(n_face) numpy.ndarray

Vector containing the indicies for the d vertex locations

averagebool, optional

If True, the function returns the average surface normal vector for each surface. If False , the function will return the normal vectors computed at the A, B, C and D vertices in a cell array {nA,nB,nC,nD}.

normalize_normalbool, optional

If True, the function will normalize the surface normal vectors. This is applied regardless of whether the average parameter is set to True or False. If False, the vectors are not normalized.

Returns:

N(n_face) numpy.ndarray or (4) list of (n_face) numpy.ndarray

Normal vector(s) for each surface. If average = True, the function returns an ndarray with the average surface normal vectos. If average = False , the function returns a cell array {nA,nB,nC,nD} containing the normal vectors computed using each vertex of the surface.

area(n_face) numpy.ndarray

The surface areas.

Examples

Here we define a set of vertices for a tensor mesh. We then index 4 vertices for an irregular quadrilateral. The function face_info is used to compute the normal vector and the surface area.

>>> from discretize.utils import face_info
>>> from discretize import TensorMesh
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import matplotlib as mpl

Define Corners of a uniform cube.

>>> h = [1, 1]
>>> mesh = TensorMesh([h, h, h])
>>> xyz = mesh.nodes

Choose the face indices,

>>> A = np.array([0])
>>> B = np.array([4])
>>> C = np.array([26])
>>> D = np.array([18])

Compute average surface normal vector (normalized),

>>> nvec, area = face_info(xyz, A, B, C, D)
>>> nvec, area
(array([[-0.70710678,  0.70710678,  0.        ]]), array([4.24264069]))

Plot surface for example 1 on mesh

>>> fig = plt.figure(figsize=(7, 7))
>>> ax = plt.subplot(projection='3d')
>>> mesh.plot_grid(ax=ax)
>>> k = [0, 4, 26, 18, 0]
>>> xyz_quad = xyz[k, :]
>>> ax.plot(xyz_quad[:, 0], xyz_quad[:, 1], xyz_quad[:, 2], 'r')
>>> ax.text(-0.25, 0., 3., 'Area of the surface: {:g} $m^2$'.format(area[0]))
>>> ax.text(-0.25, 0., 2.8, 'Normal vector: ({:.2f}, {:.2f}, {:.2f})'.format(
...     nvec[0, 0], nvec[0, 1], nvec[0, 2])
... )
>>> plt.show()

(Source code, png, pdf)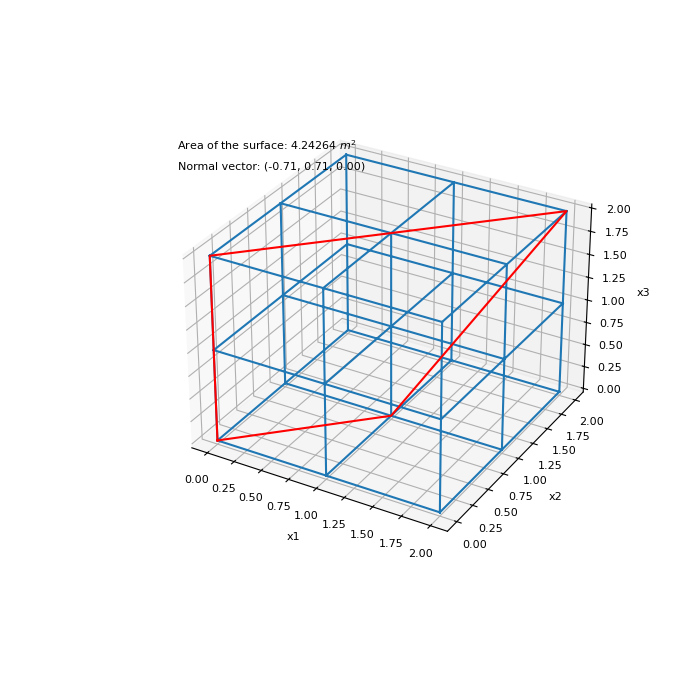

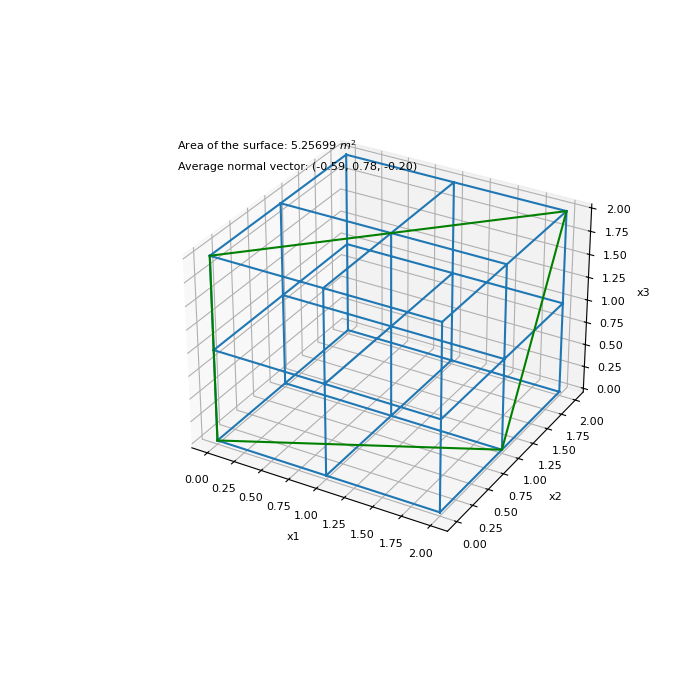
In our second example, the vertices are unable to define a flat surface in 3D space. However, we will demonstrate the face_info returns the average normal vector and an approximate surface area.

Define the face indicies >>> A = np.array([0]) >>> B = np.array([5]) >>> C = np.array([26]) >>> D = np.array([18])

Compute average surface normal vector

>>> nvec, area = face_info(xyz, A, B, C, D)
>>> nvec, area
(array([[-0.4472136 ,  0.89442719,  0.        ]]), array([2.23606798]))

Plot surface for example 2 on mesh

>>> fig = plt.figure(figsize=(7, 7))
>>> ax = plt.subplot(projection='3d')
>>> mesh.plot_grid(ax=ax)
>>> k = [0, 5, 26, 18, 0]
>>> xyz_quad = xyz[k, :]
>>> ax.plot(xyz_quad[:, 0], xyz_quad[:, 1], xyz_quad[:, 2], 'g')
>>> ax.text(-0.25, 0., 3., 'Area of the surface: {:g} $m^2$'.format(area[0]))
>>> ax.text(-0.25, 0., 2.8, 'Average normal vector: ({:.2f}, {:.2f}, {:.2f})'.format(
...     nvec[0, 0], nvec[0, 1], nvec[0, 2])
... )
>>> plt.show()

(png, pdf)