discretize.utils.volume_tetrahedron

discretize.utils.volume_tetrahedron(xyz, A, B, C, D)

Return the tetrahedron volumes for a specified set of verticies.

Let xyz be an (n, 3) array denoting a set of vertex locations. Any 4 vertex locations a, b, c and d can be used to define a tetrahedron. For the set of tetrahedra whose verticies are indexed in vectors A, B, C and D, this function returns the corresponding volumes. See algorithm: https://en.wikipedia.org/wiki/Tetrahedron#Volume

\[vol = {1 \over 6} \big | ( \mathbf{a - d} ) \cdot ( ( \mathbf{b - d} ) \times ( \mathbf{c - d} ) ) \big |\]

Parameters:

xyz(n_pts, 3) numpy.ndarray

x,y, and z locations for all verticies

A(n_tetra) numpy.ndarray of int

Vector containing the indicies for the a vertex locations

B(n_tetra) numpy.ndarray of int

Vector containing the indicies for the b vertex locations

C(n_tetra) numpy.ndarray of int

Vector containing the indicies for the c vertex locations

D(n_tetra) numpy.ndarray of int

Vector containing the indicies for the d vertex locations

Returns:

(n_tetra) numpy.ndarray

Volumes of the tetrahedra whose vertices are indexed by A, B, C and D.

Examples

Here we define a small 3D tensor mesh. 4 nodes are chosen to be the verticies of a tetrahedron. We compute the volume of this tetrahedron. Note that xyz locations for the verticies can be scattered and do not require regular spacing.

>>> from discretize.utils import volume_tetrahedron
>>> from discretize import TensorMesh
>>> import numpy as np
>>> import matplotlib.pyplot as plt
>>> import matplotlib as mpl

Define corners of a uniform cube

>>> h = [1, 1]
>>> mesh = TensorMesh([h, h, h])
>>> xyz = mesh.nodes

Specify the indicies of the corner points

>>> A = np.array([0])
>>> B = np.array([6])
>>> C = np.array([8])
>>> D = np.array([24])

Compute volume for all tetrahedra and the extract first one

>>> vol = volume_tetrahedron(xyz, A, B, C, D)
>>> vol = vol[0]
>>> vol
array([1.33333333])

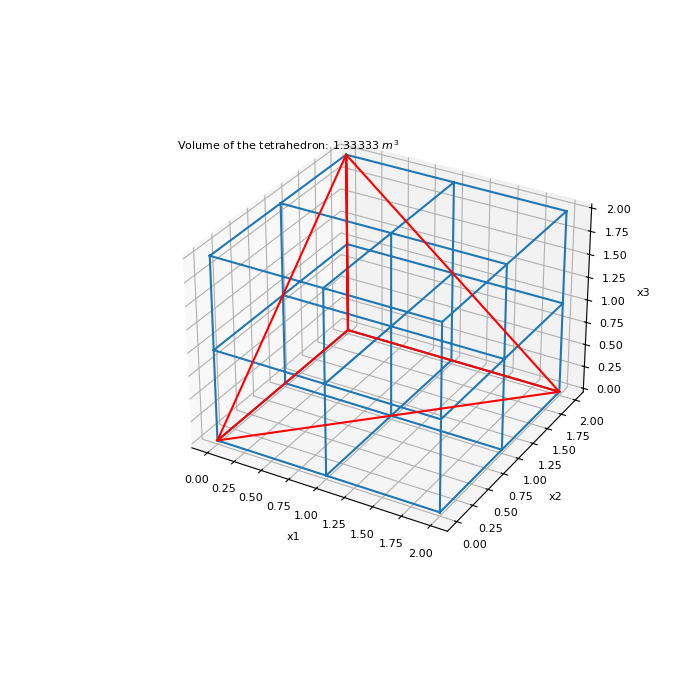
Plotting small mesh and tetrahedron

>>> fig = plt.figure(figsize=(7, 7))
>>> ax = plt.subplot(projection='3d')
>>> mesh.plot_grid(ax=ax)
>>> k = [0, 6, 8, 0, 24, 6, 24, 8]
>>> xyz_tetra = xyz[k, :]
>>> ax.plot(xyz_tetra[:, 0], xyz_tetra[:, 1], xyz_tetra[:, 2], 'r')
>>> ax.text(-0.25, 0., 3., 'Volume of the tetrahedron: {:g} $m^3$'.format(vol))
>>> plt.show()

(Source code, png, pdf)