discretize.CylindricalMesh.get_face_inner_product_deriv

CylindricalMesh.get_face_inner_product_deriv(model, do_fast=True, invert_model=False, invert_matrix=False, **kwargs)

Get a function handle to multiply a vector with derivative of face inner product matrix (or its inverse).

Let \(\mathbf{M}(\mathbf{m})\) be the face inner product matrix constructed with a set of physical property parameters \(\mathbf{m}\) (or its inverse). get_face_inner_product_deriv constructs a function handle

\[\mathbf{F}(\mathbf{u}) = \mathbf{u}^T \, \frac{\partial \mathbf{M}(\mathbf{m})}{\partial \mathbf{m}}\]

which accepts any numpy.array \(\mathbf{u}\) of shape (n_faces,). That is, get_face_inner_product_deriv constructs a function handle for computing the dot product between a vector \(\mathbf{u}\) and the derivative of the face inner product matrix (or its inverse) with respect to the property parameters. When computed, \(\mathbf{F}(\mathbf{u})\) returns a scipy.sparse.csr_matrix of shape (n_faces, n_param).

The function handle can be created for isotropic, diagonal isotropic and full tensor physical properties; see notes.

Parameters:

modelnumpy.ndarray

Parameters defining the material properties for every cell in the mesh. Inner product matrices can be constructed for the following cases:

• (n_cells) numpy.ndarray : Isotropic case. model contains a scalar physical property value for each cell.

• (n_cells, dim) numpy.ndarray : Diagonal anisotropic case. Columns are ordered np.c_[σ_xx, σ_yy, σ_zz]. This can also a be a 1D array with the same number of total elements in column major order.

• (n_cells, 3) numpy.ndarray (dim is 2) or (n_cells, 6) numpy.ndarray (dim is 3) : Full tensor properties case. Columns are ordered np.c_[σ_xx, σ_yy, σ_zz, σ_xy, σ_xz, σ_yz] This can also be a 1D array with the same number of total elements in column major order.

do_fastbool, optional

Do a faster implementation (if available).

invert_modelbool, optional

The inverse of model is used as the physical property.

invert_matrixbool, optional

Returns the inverse of the inner product matrix. The inverse not implemented for full tensor properties.

Returns:

function

The function handle \(\mathbf{F}(\mathbf{u})\) which accepts a (n_faces) numpy.ndarray \(\mathbf{u}\). The function returns a (n_faces, n_params) scipy.sparse.csr_matrix.

Notes

Let \(\mathbf{M}(\mathbf{m})\) be the face inner product matrix (or its inverse) for the set of physical property parameters \(\mathbf{m}\). And let \(\mathbf{u}\) be a discrete quantity that lives on the faces. get_face_inner_product_deriv creates a function handle for computing the following:

\[\mathbf{F}(\mathbf{u}) = \mathbf{u}^T \, \frac{\partial \mathbf{M}(\mathbf{m})}{\partial \mathbf{m}}\]

The dimensions of the sparse matrix constructed by computing \(\mathbf{F}(\mathbf{u})\) for some \(\mathbf{u}\) depends on the constitutive relation defined for each cell. These cases are summarized below.

Isotropic Case: The physical property for each cell is defined by a scalar value. Therefore \(\mathbf{m}\) is a (n_cells) numpy.ndarray. The sparse matrix output by computing \(\mathbf{F}(\mathbf{u})\) has shape (n_faces, n_cells).

Diagonal Anisotropic Case: In this case, the physical properties for each cell are defined by a diagonal tensor

\[\begin{split}\Sigma = \begin{bmatrix} \sigma_{xx} & 0 & 0 \\ 0 & \sigma_{yy} & 0 \\ 0 & 0 & \sigma_{zz} \end{bmatrix}\end{split}\]

Thus there are dim * n_cells physical property parameters and \(\mathbf{m}\) is a (dim * n_cells) numpy.ndarray. The sparse matrix output by computing \(\mathbf{F}(\mathbf{u})\) has shape (n_faces, dim * n_cells).

Full Tensor Case: In this case, the physical properties for each cell are defined by a full tensor

\[\begin{split}\Sigma = \begin{bmatrix} \sigma_{xx} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{xy} & \sigma_{yy} & \sigma_{yz} \\ \sigma_{xz} & \sigma_{yz} & \sigma_{zz} \end{bmatrix}\end{split}\]

Thus there are 6 * n_cells physical property parameters in 3 dimensions, or 3 * n_cells physical property parameters in 2 dimensions, and \(\mathbf{m}\) is a (n_params) numpy.ndarray. The sparse matrix output by computing \(\mathbf{F}(\mathbf{u})\) has shape (n_faces, n_params).

Examples

Here, we construct a 4 cell by 4 cell tensor mesh. For our first example we consider isotropic physical properties; that is, the physical properties of each cell are defined a scalar value. We construct the face inner product matrix and visualize it with a spy plot. We then use get_face_inner_product_deriv to construct the function handle \(\mathbf{F}(\mathbf{u})\) and plot the evaluation of this function on a spy plot.

>>> from discretize import TensorMesh
>>> import matplotlib.pyplot as plt
>>> import numpy as np
>>> import matplotlib as mpl
>>> mpl.rcParams.update({'font.size': 14})
>>> rng = np.random.default_rng(45)
>>> mesh = TensorMesh([[(1, 4)], [(1, 4)]])

Define a model, and a random vector to multiply the derivative with, then we grab the respective derivative function and calculate the sparse matrix,

>>> m = rng.random(mesh.nC)  # physical property parameters
>>> u = rng.random(mesh.nF)  # vector of shape (n_faces)
>>> Mf = mesh.get_face_inner_product(m)
>>> F = mesh.get_face_inner_product_deriv(m)  # Function handle
>>> dFdm_u = F(u)

Spy plot for the inner product matrix and its derivative

>>> fig = plt.figure(figsize=(15, 5))
>>> ax1 = fig.add_axes([0.05, 0.05, 0.3, 0.85])
>>> ax1.spy(Mf, ms=6)
>>> ax1.set_title("Face Inner Product Matrix (Isotropic)", fontsize=14, pad=5)
>>> ax1.set_xlabel("Face Index", fontsize=12)
>>> ax1.set_ylabel("Face Index", fontsize=12)
>>> ax2 = fig.add_axes([0.43, 0.05, 0.17, 0.8])
>>> ax2.spy(dFdm_u, ms=6)
>>> ax2.set_title(
...     r"$u^T \, \dfrac{\partial M(m)}{\partial m}$ (Isotropic)",
...     fontsize=14, pad=5
... )
>>> ax2.set_xlabel("Parameter Index", fontsize=12)
>>> ax2.set_ylabel("Face Index", fontsize=12)
>>> plt.show()

(Source code, png, pdf)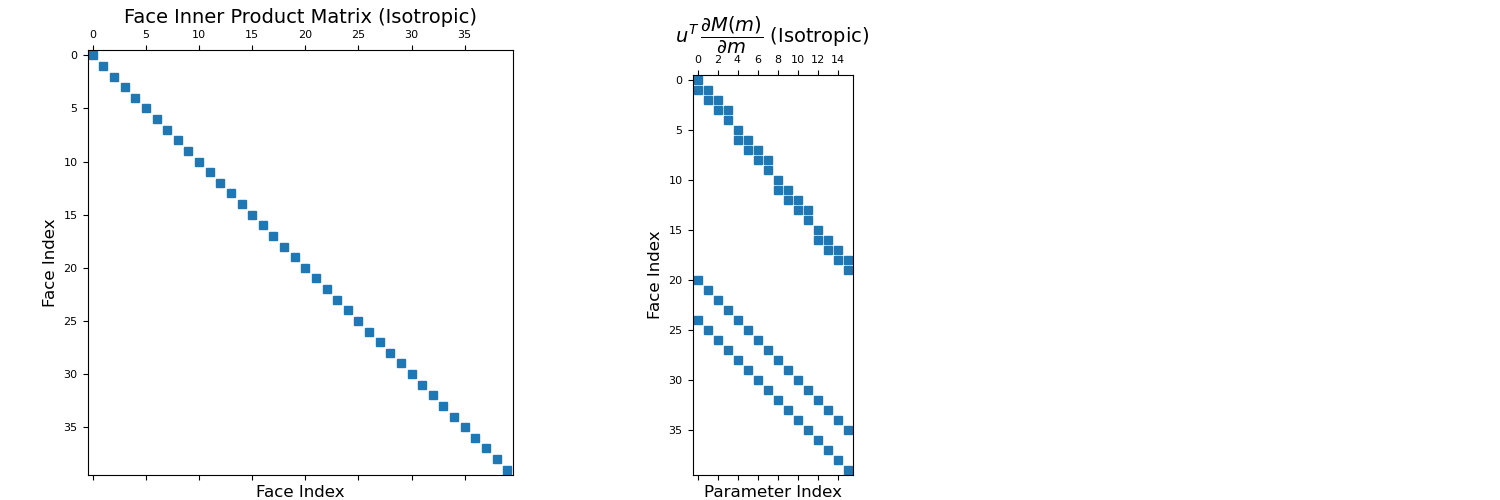

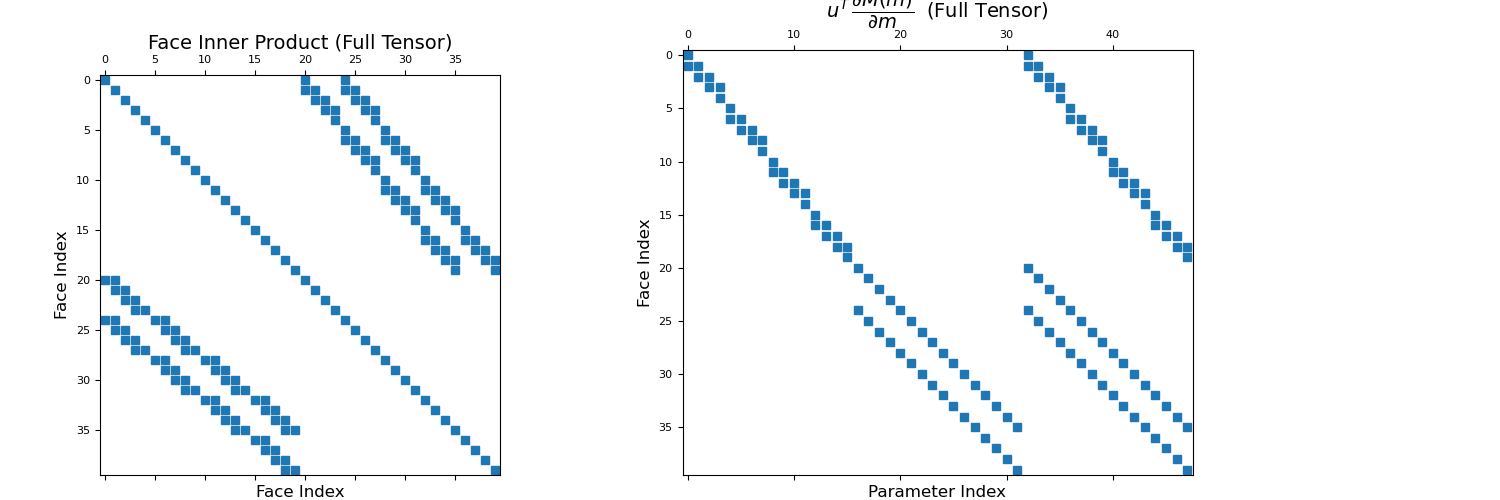
For our second example, the physical properties on the mesh are fully anisotropic; that is, the physical properties of each cell are defined by a tensor with parameters \(\sigma_1\), \(\sigma_2\) and \(\sigma_3\). Once again we construct the face inner product matrix and visualize it with a spy plot. We then use get_face_inner_product_deriv to construct the function handle \(\mathbf{F}(\mathbf{u})\) and plot the evaluation of this function on a spy plot.

>>> m = rng.random((mesh.nC, 3))  # anisotropic physical property parameters
>>> u = rng.random(mesh.nF)     # vector of shape (n_faces)
>>> Mf = mesh.get_face_inner_product(m)
>>> F = mesh.get_face_inner_product_deriv(m)  # Function handle
>>> dFdm_u = F(u)

Plot the anisotropic inner product matrix and its derivative matrix,

>>> fig = plt.figure(figsize=(15, 5))
>>> ax1 = fig.add_axes([0.05, 0.05, 0.3, 0.8])
>>> ax1.spy(Mf, ms=6)
>>> ax1.set_title("Face Inner Product (Full Tensor)", fontsize=14, pad=5)
>>> ax1.set_xlabel("Face Index", fontsize=12)
>>> ax1.set_ylabel("Face Index", fontsize=12)
>>> ax2 = fig.add_axes([0.4, 0.05, 0.45, 0.85])
>>> ax2.spy(dFdm_u, ms=6)
>>> ax2.set_title(
...     r"$u^T \, \dfrac{\partial M(m)}{\partial m} \;$ (Full Tensor)",
...     fontsize=14, pad=5
... )
>>> ax2.set_xlabel("Parameter Index", fontsize=12)
>>> ax2.set_ylabel("Face Index", fontsize=12)
>>> plt.show()

(png, pdf)