discretize.operators.DiffOperators.edges#
- property DiffOperators.edges#
Gridded edge locations.
This property returns a numpy array of shape (n_edges, dim) containing gridded locations for all edges in the mesh.
For structured meshes, the first row corresponds to the bottom-front-leftmost x-edge. The output array returns the x-edges, then the y-edges, then the z-edges; i.e. mesh.edges is equivalent to np.r_[mesh.edges_x, mesh.edges_y, mesh.edges_z] . For each edge type, the locations are ordered along the x, then y, then z directions.
- Returns:
- (
n_edges,dim)numpy.ndarrayoffloat Gridded edge locations
- (
Examples
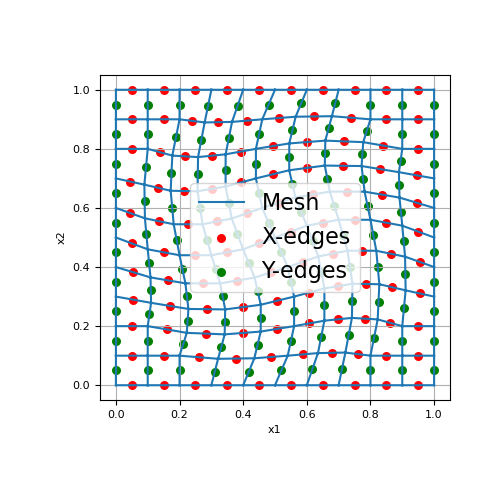
Here, we provide an example of a minimally staggered curvilinear mesh. In this case, the x and y-edges have normal vectors that are primarily along the x and y-directions, respectively.
>>> from discretize import CurvilinearMesh >>> from discretize.utils import example_curvilinear_grid, mkvc >>> from matplotlib import pyplot as plt
>>> x, y = example_curvilinear_grid([10, 10], "rotate") >>> mesh1 = CurvilinearMesh([x, y]) >>> edges = mesh1.edges >>> x_edges = edges[:mesh1.n_edges_x] >>> y_edges = edges[mesh1.n_edges_x:]
>>> fig1 = plt.figure(figsize=(5, 5)) >>> ax1 = fig1.add_subplot(111) >>> mesh1.plot_grid(ax=ax1) >>> ax1.scatter(x_edges[:, 0], x_edges[:, 1], 30, 'r') >>> ax1.scatter(y_edges[:, 0], y_edges[:, 1], 30, 'g') >>> ax1.legend(['Mesh', 'X-edges', 'Y-edges'], fontsize=16) >>> plt.plot()
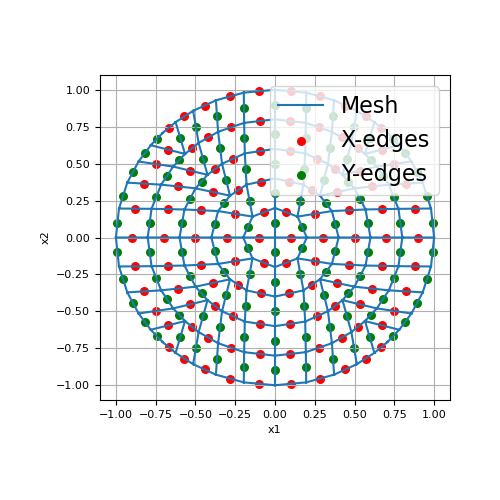
Here, we provide an example of a highly irregular curvilinear mesh. In this case, the y-edges are not defined by normal vectors along a particular direction.
>>> x, y = example_curvilinear_grid([10, 10], "sphere") >>> mesh2 = CurvilinearMesh([x, y]) >>> edges = mesh2.edges >>> x_edges = edges[:mesh2.n_edges_x] >>> y_edges = edges[mesh2.n_edges_x:]
>>> fig2 = plt.figure(figsize=(5, 5)) >>> ax2 = fig2.add_subplot(111) >>> mesh2.plot_grid(ax=ax2) >>> ax2.scatter(x_edges[:, 0], x_edges[:, 1], 30, 'r') >>> ax2.scatter(y_edges[:, 0], y_edges[:, 1], 30, 'g') >>> ax2.legend(['Mesh', 'X-edges', 'Y-edges'], fontsize=16) >>> plt.show()